Kirchhoff’s Current Law (KCL) is one of the power tools used to analyze a large variety of electric circuits. This law was given by the German physicist Gustav Robert Kirchhoff in 1847. Kirchhoff’s current law or KCL is also known as Kirchhoff’s first law. This law is based on the law of conversation of charge which states that the algebraic sum of all charges in a closed system does not change. In other words, the electric charge can neither be created nor destroyed.

Statement of Kirchhoff’s Current Law
Kirchhoff’s Current Law states that
In a closed electric circuit, the algebraic sum of currents entering a node or a junction is equal to the algebraic sum of currents leaving that node.
In other words, at a node in a circuit, the total incoming electric current is equal to the total outgoing current.
Mathematically, we can write this statement as
$$∑I_{in} =∑I_{out}$$
The KCL can be stated as follows,
The algebraic sum of incoming currents and outgoing currents at a node in an electric circuit is equal to zero i.e.,
$$∑I_{in} +∑I_{out} =0$$
For example, consider a part of an electric circuit shown in the following figure.
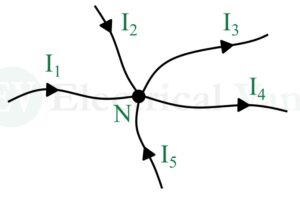
Here, N is a node or a junction having 5 branches connected to it. When we apply KCL to this node, we get the following KCL equation,
$$I_1+I_2+I_5=I_3+I_4$$
Where I1, I2, and I5 are the incoming currents, and I3 and I4 are the outgoing currents.
This expression can also be written as
$$I_1+I_2+I_5+(-I_3 )+(-I_4 )=0$$
$$⇒I_1+I_2-I_3-I_4+I_5=0$$
It is a convention followed while writing a KCL equation for a node that the currents entering the node are taken as positive and the currents leaving the node are taken as negative. However, we can also follow its opposite as well.
In generalized form, if a node in an electric circuit has N total branches connected to it, then according to KCL, we can write,
$$∑_{k=1}^N i_k =0$$
Important Points About KCL
The following are some key points related to the Kirchhoff’s current law (KCL):
- KCL is based on the principle of conservation of electric charge, which states that the total charge within an electric circuit remains constant.
- In an electric circuit, a node is a point where two or more circuit elements join together.
- A branch in an electric circuit is the path connecting two nodes.
- In KCL, it is a convention that the incoming currents are taken as positive, while the outgoing currents are taken as negative.
- The sum of electric currents at a node is computed algebraically, which means both the magnitude and direction of the currents are taken into account.
Combining Current Source Using KCL
We can use Kirchhoff’s current law to combine multiple current sources connected in parallel. Where the current supplied by the combined source is the algebraic sum of currents supplied by the individual current sources.
For example, consider an electric circuit having three current sources connected in parallel as shown in the following figure. Applying KCL at the node a, we get,
Applying KCL at the node a, we get,
$$I_1+I_2=I_T+I_3$$
Therefore, the total current of the combined current source is,
$$I_T=I_1+I_2+I_3$$
It is important to note that if two different current sources, say I1 and I2 cannot be connected in series, unless I1 = I2. Otherwise, it will violate Kirchhoff’s current law.
This is all about Kirchhoff’s current law (KCL), its statement, equation, and applications. Let us now understand the application of KCL in writing nodal equations in an electric circuit.
Examples Based on KCL
Example (1) – Determine the total current flowing through the resistor R3 in the following circuit.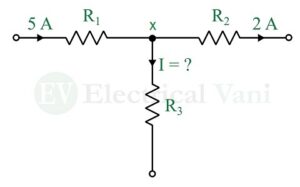
Solution – Applying KCL at the node x, we get,
$$5=I+2$$
$$∴I=5-2=3\text{ A}$$
Example (2) – Find the current I through the 1 Ω resistor in the following circuit.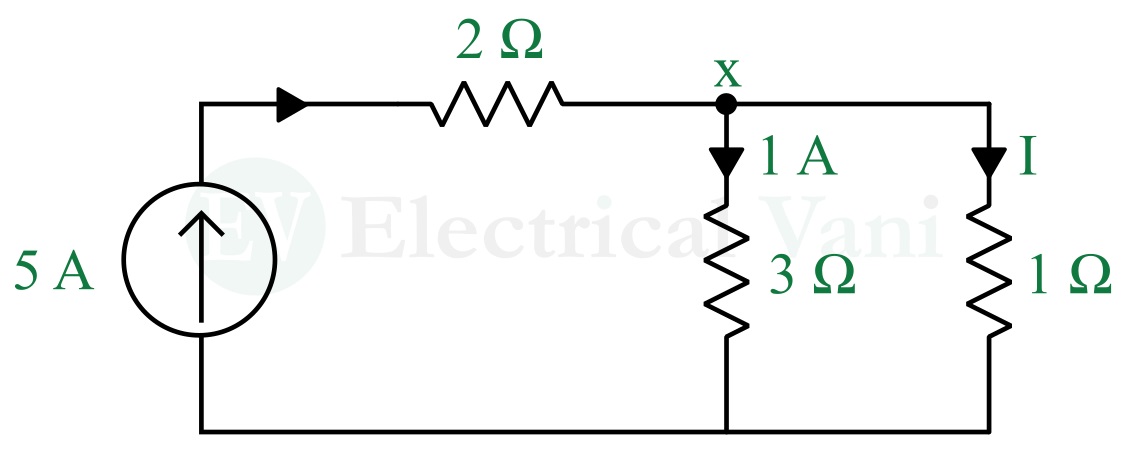
Solution – Applying KCL at the node x, we get,
$$5=1+I$$
$$∴I=5-1=4\text{ A}$$
These examples illustrate the application of KCL in circuit analysis.
Conclusion
In this article, we have studied about the Kirchhoff’s current law (KCL). Here, we have covered all the important concepts related to KCL such as statement, equation, convention, applications, and examples. Still, if you have any questions related to this topic, kindly let me know in the comment section.