In this article, we will learn about Ohm’s law, its statement, formula, and solved examples based on it. In electric circuits, Ohm’s law is a fundamental tool for analyzing electric circuits. This law provides a relationship between the voltage, current, and resistance of an electric conductor. Let’s start our study with the definition or statement of Ohm’s law.

Ohm’s Law Definition
Ohm’s law is the most fundamental circuit law stated by the German Scientist George Simon Ohm. This law states that
The voltage applied across a conductor or wire is directly proportional to the electric current flowing through it.
This statement holds true only if the physical conditions like area, length, temperature, etc. of the conductor do not change.
If the physical conditions of the conductor are not constant, then Ohm’s law cannot be applied to that conductor.
For example, we cannot use Ohm’s law to analyze the internal circuit of an incandescent lamp. It is because the temperature and hence the resistance of the lamp filament under the OFF state and ON state is different. In practice, under normal operating conditions, the resistance of the lamp filament is around 10 times its resistance in the OFF state.
Ohm’s Law Formula
From the statement of the Ohm’s law, we can write,
$$V∝I$$
Where, V is the voltage applied across the conductor and I is the resulting current flowing through the conductor.
Also,
$$V=IR$$
Where, R is a constant of proportionality, known as resistance of the conductor.
Let us consider a conductor as shown in the following figure.
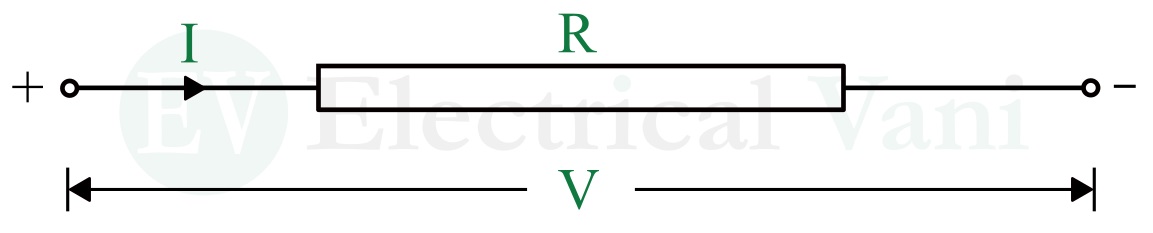
The voltage or potential difference applied across the conductor is V volts, the current flowing through the conductor is I amperes, and R ohms is the resistance of the conductor, then, we can write,
$$V=IR$$
Also, the current through the conductor is given by,
$$I=\frac{V}{R}$$
The resistance of the conductor can be given by,
$$R=\frac{V}{I}$$
If any two of the three parameters are known for a given conductor, then the third one can be calculated using any of the above Ohm’s law equations.
Ohm’s Law Triangle
The Ohm’s law triangle is a graphical representation of the Ohm’s law equations. This triangle is shown in the following figure.
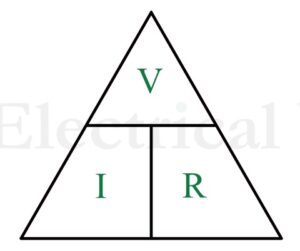
Let us now take some solved numerical examples to understand the application of Ohm’s law.
Examples based on Ohm’s Law
Numerical Example (1) – What is the value of resistance R of a copper wire if the voltage drop across the conductor is 240 V and the current through the wire is 2.5 A?
Solution – From the problem, we have,
$$V=240 V$$
$$I=2.5 A$$
Then, according to Ohm’s law,
$$R=\frac{V}{I}=\frac{240}{2.5}$$
$$∴R=96 Ω$$
Thus, the resistance of the given copper wire is 96 ohms.
Numerical Example (2) – If a conductor strip has a resistance of 25 ohms, and the voltage across it is 220 V. Find the current flowing through the strip.
Solution – We are given the following,
$$R=25 Ω$$
$$V=220 V$$
Applying Ohm’s law, we get the current as,
$$I=\frac{V}{R}=\frac{220}{25}$$
$$∴I=8.8 A$$
Hence, the given conductor strip is carrying a current of 8.8 A.
Numerical Example (3) – If a cable is carrying a current of 6 A and its resistance is 5 ohms. What will be the voltage drop across the cable?
Solution – Given,
$$I=6 A$$
$$R=5 Ω$$
According to Ohm’s law, the voltage drop across the cable will be,
$$V=IR=6×5$$
$$V=30 V$$
Hence, the voltage drop across the cable is 30 volts.
Practice Problems based on Ohm’s Law
Try solving the following numerical problems based on Ohm’s law formula.
Q. 1 – An aluminum coil has a resistance of 10 Ω and a voltage drop across it is 260 V. Find the current flowing through the coil.
Q. 2 – A copper wire has a resistance of 50 Ω. Find the voltage drop across the wire if it carries a current of 4.5 A.
Q. 3 – When an electric heater is connected to an electric supply of 220 volts, it draws a current of 16 A. Calculate the resistance of the filament of the heater, neglecting the resistance of connecting wires and cables.