In this article, I will teach you about the relation between current and drift velocity. Both current and drift velocity are two important terms related to electrons in the field of current electricity. Electric current is the rate of flow of electrons in a conductor, whereas the drift velocity is the average velocity of electrons through the conductor. Hence, it is important to study the relation between current and drift velocity to understand other important concepts of current electricity.

Before discussing the relation between current and drift velocity. Let us first get an overview of current and drift velocity individually.
What is Current?
Current or electric current is the flow of electrons through a conducting material in a specific direction. It is measured as the rate of flow of electrons.
Current is usually denoted by the letter I or i. The SI unit of electric current is Ampere (A) which is coulombs per second.
The strength of electric current flowing through a conductor is given by,
$$I=\frac{Q}{t}$$
In differential form,
$$i=\frac{\text{d}q}{\text{d}t}$$
Where Q is the electric charge measured in coulomb and t is the time in seconds.
What is Drift Velocity?
In a metallic conductor, there is a large number of free electrons that travel randomly within the body of the conductor. At normal room temperature, the speed of these randomly moving electrons is very high, around the order of 105 m/s.
When the free electrons move randomly, they repeatedly collide with the atoms of the metal, and at each collision their direction of movement changes. Therefore, the average movement of all the electrons in the conductor is zero.
Thus, in the absence of an electric field, the net movement of electrons in a particular direction is zero. As a result, there is no current flow through the conductor.
But in case, when a potential difference or voltage is applied across the conductor, and an electric field is established over the entire length of the conductor. This electric field has a certain direction from the positive potential point to the negative potential point. Consequently, the electric field forces the free electrons to move towards the point of positive potential.
During the movement towards the positive potential point, the electrons collide with atoms of the metal conductor. At each collision, the free electrons lose the extra energy gained due to the applied electric field.
Hence, the free electrons continuously move towards the point of positive potential with a constant velocity. This constant velocity of electrons is called their drift velocity.
Therefore, the drift velocity can be defined as follows:
The average constant velocity of electrons in a metallic conductor with which they move towards the point of positive potential under the influence of an external electric field is called drift velocity. The drift velocity is commonly represented by the symbol “vd”.
Mathematically, the drift velocity of electrons is given by,
$$\text{Drift Velocity},v_d=\frac{l}{t}$$
Where, l is the length of the conductor in meters and t is the time taken to cross this length in seconds. Hence, the unit of drift velocity is m/s.
This is all about the basics of electric current and drift velocity. Let us now learn about the relation between current and drift velocity.
Relation between Current and Drift Velocity
As we know, the drift velocity is the average velocity of electrons in a metallic conductor. While the electric current is the directed flow of electrons in the metallic conductor. Hence, both these concepts are related to each other. In this section, we will derive the mathematical expression representing the relation between current and drift velocity.
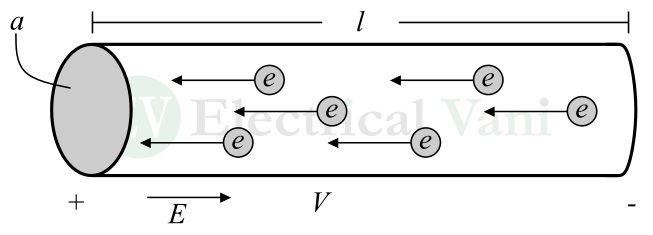
Consider a metallic conductor of length l m and area of cross-section a m2. Then, the volume of the conductor will be,
$$\text{Volume of conductor}=l × a$$
If the electron density i.e., number of electrons per unit volume of the conductor is n. Then, the total number of electrons in the conductor will be,
$$\text{Total number of electrons}=n×l×a$$
As we know, the charge on an electron is given by e, where e = 1.6 × 10-19 C. Then, the total charge in the conductor is given by,
$$Q=\text{Total electrons}×e$$
For the given conductor, we get,
$$Q=nla×e$$
Consider we apply a potential difference of V volts across the conductor. Which causes an electric field E to be established over the entire length of the conductor. This electric field causes electrons to move in the conductor.
The time taken by each electron to cross the length of the conductor is given by,
$$t=\frac{l}{v_d}$$
Also, we know that the electric current is given by,
$$I=\frac{Q}{t}$$
Substituting the value of Q and t in the expression, we get,
$$I=\frac{nlae}{(l⁄v_d )}$$
Rearranging this equation, we get,
$$I=neav_d$$
This expression gives the relation between current and drift velocity.
For a given conductor, l, n, a, and, e are constants. Thus,
$$I∝v_d$$
That means the electric current in a conductor is directly proportional to the drift velocity of electrons in the conductor.
Numerical Examples Based on Relation between Current and Drift Velocity
Example (1) – A copper wire of length 10 m and a cross-sectional area of 2.5 mm2 carries a current of 6 A. If the number of free electrons in the wire is 8.5 × 1028 m-3. Calculate the drift velocity of the electrons in the copper wire.
Solution – Given parameters are,
$$\text{Length of wire},l=10\text{ m}$$
$$\text{Area of wire},a=2\text{ mm}^2=2×10^{-6}\text{ m}^2$$
$$\text{Electron density},n=8.5×10^{28} \text{ m}^{-3}$$
$$\text{Current},I=6\text{ A}$$
Then, using the relation between current and drift velocity, we have,
$$I=neav_d$$
Therefore, the drift velocity is given by,
$$v_d=\frac{I}{nea}$$
Putting the values of parameters, we get,
$$v_d=\frac{6}{(8.5×10^{28}×1.6×10^{-19}×2×10^{-6} )}$$
$$∴v_d=2.21×10^{-4} \text{ ms}^{-1}$$
Hence, the drift velocity of the free electrons through the given copper wire is 2.21 × 10-4 m/s.
Example (2) – A conductor wire carries a current of 15 A. The cross-sectional area of the conductor wire is 4 × 10-6 m2. Calculate the average drift velocity of electrons, if the electron density is 8.5 × 1028 m-3.
Solution – Given data is,
$$\text{Current},I=15\text{ A}$$
$$\text{Cross section area},a=4×10^{-6} \text{ m}^2$$
$$\text{Electron density},n=8.5×10^{28} \text{ m}^{-3}$$
Then, using the relation between current and drift velocity, we get,
$$I=neav_d$$
Thus, the drift velocity will be,
$$v_d=\frac{I}{nea}$$
Substituting the values of variables, we get,
$$v_d=\frac{15}{(8.5×10^{28}×1.6×10^{-19}×4×10^{-6} )}$$
$$∴v_d=2.76×10^{-4} \text{ ms}^{-1}$$
Hence, in this conductor, the drift velocity of electrons is 2.76 × 10-4 m/s.
Conclusion
In conclusion, the electric current and drift velocity are two related concepts. Where, the electric current is the directed movement of free electrons, while the drift velocity is the average velocity of the free electrons in the conductor.
In this article, I have explained the relation between current and drift velocity. Also, I have included some solved numerical examples based on the mathematical expression of the relation between current and drift velocity.
If you have any queries related to this topic. Please let me know in the comment section. I will answer shortly.