Voltage and Turns Ratio of Transformer

In an electrical transformer, there are two important parameters namely, voltage transformation ratio and turns ratio used to determine its operation, whether step-up or step-down. These two ratios are also important for performing various transformer calculations and analyses. In this article, we will discuss the definition and formula of voltage and turns ratio along with solved examples based on them.

Voltage Transformation Ratio of Transformer

For an electrical transformer, the ratio of output (secondary winding) voltage V_2­ to input (primary winding) voltage V₁ is known as the voltage transformation ratio. It is usually denoted by the letter K and is given by,

$$K=\frac{V_2}{V_1}$$

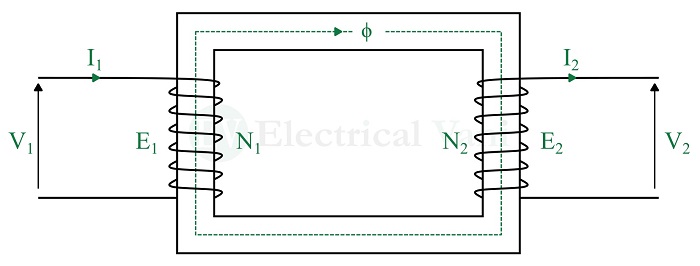
For an ideal transformer, we have V₁ = E₁ and V_2­ = E₂, where E₁ and E₂ are the EMFs induced in the primary and secondary windings of the transformer. Therefore, the voltage transformation ratio of an ideal transformer can be given by,

$$K=\frac{V_2}{V_1}=\frac{E_2}{E_1}$$

Also, in an ideal transformer, there are no losses inside the transformer. Thus, the input volt-amperes and output volt-amperes are equal i.e.,

$$V_1 I_1=V_2 I_2$$

Hence, the voltage ratio of the ideal transformer can also be written as,

$$K=\frac{V_2}{V_1}=\frac{E_2}{E_1}=\frac{I_1}{I_2}$$

From this expression, it is clear that the currents in a transformer in inverse ratio of the voltages.

So, this is all about the voltage transformation ratio of the transformer. Let us now discuss the turns ratio of the transformer.

Turns Ratio of Transformer

Turns ratio of a transformer is defined as the ratio of primary winding turns and secondary winding turns. It is generally denoted by the letter a and is given by,

$$a=\frac{N_1}{N_2}$$

Since, in a transformer, the induced emf in a winding is directly proportional to the number of turns in it i.e.,

$$E∝N$$

Therefore, the turns ratio can be written as,

$$a=\frac{N_1}{N_2}=\frac{E_1}{E_2}$$

For an ideal transformer, E₁ = V₁, E₂ = V₂, and V₁I₁ = V₂I₂, thus,

$$a=\frac{N_1}{N_2} =\frac{E_1}{E_2} =\frac{V_1}{V_2} =\frac{I_2}{I_1} =\frac{1}{K}$$

So, this is all about the turns ratio of a transformer.

Let us now see some solved examples based on these two ratios of transformer.

Numerical Example

An 11kV/440V, 20 kVA transformer has 80 turns in the secondary winding. Calculate the following:

• Voltage transformation ratio (K)
• Primary winding turns (N₁)
• Turns ratio (a)
• Primary and secondary winding full load currents (I₁ and I₂)

Solution – Given data,

$$V_1=11 kV=11000 V$$

$$V_2=440 V$$

$$N_2=80$$

Voltage transformation ratio:

$$K=\frac{V_2}{V_1} =\frac{440}{11000}=0.04$$

Primary winding turns:

$$K=\frac{V_2}{V_1} =\frac{N_2}{N_1}$$

$$⇒N_1=\frac{N_2}{K}=\frac{80}{0.04}=2000$$

Turns ratio:

$$a=\frac{N_1}{N_2} =\frac{2000}{80}=25$$

Primary and secondary full-load current:

$$V_1 I_1=V_2 I_2=20 kVA$$

$$\text{Primary current }I_1=\frac{20k}{V_1} =\frac{20k}{11k}=1.82 A$$

$$\text{Secondary current }I_2=\frac{20k}{V_2} =\frac{20k}{440}=45.45 A$$

Conclusion

So, this is all about the voltage transformation and the turns ratio of an electrical transformer. In this article, we have discussed about the definition, formula, and examples of voltage transformation and turns ratio of the transformer.