In digital electronics, there are three basic logic gates namely, OR Gate, AND Gate, and NOT Gate. These three logic gates are widely used to implement logic functions and design different types of digital electronic systems. Using these basic logic gates, we can easily implement digital circuits like multiplexers, demultiplexers, adders, subtractors, encoders, decoders, flip-flops, and more. Hence, the knowledge of these three logic gates is crucial to understanding the rest parts of digital electronics and circuits. In simple terms, basic logic gates i.e., OR gate AND gate, and NOT gate are the fundamental building blocks of all digital systems and circuits. Hence, it is important to understand the operation of these logic gates.

In this article, I will cover all the important concepts like their definition, truth table, logic symbol, Boolean expression, etc. related to these three basic logic gates. So, let’s start with the basic introduction to logic gates.
What is a Logic Gate?
An electronic circuit that is used to implement and perform a logical operation or function like comparison is known as a logic gate. A logic gate is typically constructed from diodes, transistors, resistors, etc. These components are connected together in such a way that the result circuit can perform a logical operation.
Types of Logic Gates
In digital electronics, there are several types of logic gates depending on their operational behavior. All these logic gates are broadly classified into the following three categories:
- Basic Logic Gates – OR Gate, AND Gate, and NOT Gate
- Universal Logic Gates – NAND Gate and NOR Gate
- Derived Logic Gates – XNOR Gate and XOR Gate
In this article, we explore the three basic logic gates i.e., OR gate, AND gate, and NOT gate. Let’s start our learning with the understanding of the OR gate.
What is OR Gate?
OR Gate is a type of basic logic gate that can have two or more inputs but only one output. The output of the OR gate is a logic 1 or high state if any of its inputs is in the logic 1 or high state. The output of the OR gate is logic 0 or low state, only when its all inputs are logic 0 or low.
In other words, we can define an OR gate as a logic gate whose output is logic 1 or high, even if one of its inputs is logic 1 or high.
OR Gate Symbol
The logic symbols of two-input and three-input OR gates are shown in the following figure.

In these symbols, A, B, and C are the input variables, while Y is the output variable.
OR Gate Truth Table
The truth table is a table that describes the output of a logic gate for a specific combination of inputs.
The truth table of a two-input OR gate is given below:
|
Inputs |
Output | |
| A | B |
Y |
|
0 |
0 | 0 |
| 0 | 1 |
1 |
|
1 |
0 | 1 |
| 1 | 1 |
1 |
The truth table of a three-input OR gate is given below:
|
Inputs |
Output | ||
| A | B | C |
Y |
|
0 |
0 | 0 | 0 |
| 0 | 0 | 1 |
1 |
|
0 |
1 | 0 | 1 |
| 0 | 1 | 1 |
1 |
|
1 |
0 | 0 | 1 |
| 1 | 0 | 1 |
1 |
|
1 |
1 | 0 | 1 |
| 1 | 1 | 1 |
1 |
OR Gate Boolean Expression
The Boolean expression is a logical function that describes the relationship between inputs and output of a logic gate. We can directly derive the Boolean expression of a logic gate from its truth table.
The Boolean expression of a two-input OR gate can be derived from its truth table given above and it is given below.
Y = A + B
Here, A and B are the input variables, Y is the output variable, and the sign “+” denotes the OR operation.
Similarly, the Boolean expression of a three-input OR gate can be derived from its truth table and it is given below.
Y = A + B + C
Here, A, B, and C are the input variables and Y is the output variable.
Hence, this is all about the OR gate. Let us now explore the AND gate and its concepts.
What is AND Gate?
AND gate is also a type of basic logic gate. It can take two or more inputs and give only one output. The output of an AND gate is logic 1 or high state, only when its all inputs are in logic 1 or high state. For all other input combinations, the output of an AND gate is logic 0 or low state.
In other words, an AND gate is defined as a logic gate whose output is logic 1 or high, if and only if all its inputs are logic 1 or high.
AND Gate Symbol
The logic symbols of two-input and three-input AND gates are depicted in the following figure.

Here, A, B, and C are the input variables and Y is the output variable.
AND Gate Truth Table
The following is the truth table of a two-input AND gate:
|
Inputs |
Output | |
| A | B |
Y |
|
0 |
0 | 0 |
| 0 | 1 |
0 |
|
1 |
0 | 0 |
| 1 | 1 |
1 |
The following is the truth table of a three-input AND gate:
|
Inputs |
Output | ||
| A | B | C |
Y |
|
0 |
0 | 0 | 0 |
| 0 | 0 | 1 |
0 |
|
0 |
1 | 0 | 0 |
| 0 | 1 | 1 |
0 |
|
1 |
0 | 0 | 0 |
| 1 | 0 | 1 |
0 |
|
1 |
1 | 0 | 0 |
| 1 | 1 | 1 |
1 |
From these truth tables, it can be observed that the output of an AND gate is logic 1 or high, only when all its inputs are logic 1 or high. For the rest input combination, the output is logic 0 or low.
AND Gate Boolean Expression
The Boolean expression or Boolean function of a two-input AND gate is given below:
Y = A . B
Here, A and B are input variables, Y is the output variable, and the symbol “.” denotes the logic AND operation.
Similarly, the Boolean expression of a three-input AND gate is given below:
Y = A . B . C
Here, A, B, and C are the input variables, and Y is the output variable.
Hence, this is all about AND gate. Let us now learn about the logic NOT gate.
What is NOT Gate?
NOT Gate, also called Inverter Gate, is the third type of basic logic gate in digital electronics. It is a logic gate with one input and one output. The output of the NOT gate is in logic 0 or low state when its input is in logic 1 or high state, and vice-versa.
Since the NOT gate performs an inversion operation, it is also called an inverter or inverter gate.
NOT Gate Symbol
The logic symbol of the NOT gate is depicted in the following figure.
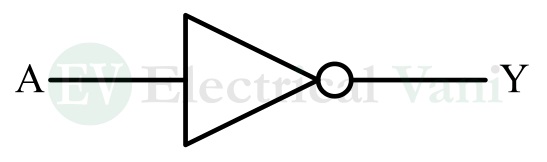
It has only one input line ‘A’, and one output line ‘Y’.
The bubble symbol right corner of the triangle denotes the inversion operation and is called an inversion bubble.
NOT Gate Truth Table
The following is the truth table of the NOT gate:
|
Input (A) |
Output (Y) |
| 0 |
1 |
|
1 |
0 |
Hence, it can be seen that the NOT gate produces an opposite output state of its input.
NOT Gate Boolean Expression
The Boolean expression or Boolean function of the NOT gate is given below.
$$Y=A’=\overline{A}$$
Here, A is the input variable, Y is the output variable, and the prime (`) or bar (-) over the input variable A denotes the inversion operation.
Now, after studying the theory of all three basic logic gates, let us now dive into the applications of logic gates.
Applications of Logic Gates
The basic logic gates (OR gate, AND gate, and NOT gate) are used in the following applications:
- Logic gates are used to implement logical functions like comparison of numbers, etc.
- Logic gates are used to design systems that can make decisions to automate the processes, as in industrial automation.
- Logic gates are widely used to design circuitry of digital calculators, computers, and other digital devices.
- Logic gates are also used in digital measuring instruments like digital multimeters.
- Logic gates are extensively used in designing communication systems for information transmission.
Hence, these are some key applications of logic gates. However, the list of applications of logic gates can never end here.
Conclusion
In this article, I have explained the three basic logic gates along with their symbol, truth table, and Boolean function. Also, I have included a list of applications for these gates. In conclusion, the AND gate, OR gate, and NOT gate are the fundamental logic gates in digital systems used to implement and realize the logical functions to perform tasks in real life. These three logic gates are considered the backbone of all digital circuits and systems.
If you have any queries related to these logic gates, please let me know in the comment section. I will answer shortly.