In this article, we shall introduce a new linear passive circuit element, the capacitor. The capacitor is a passive circuit element used in a variety of electronic circuits. It does not dissipate energy like a resistor, but stores energy that can be retrieved at a later point in time. That’s why in electronics, the capacitor is known as a storage element.

What is a Capacitor?
In electronics, a capacitor is a passive circuit element used to store electrical energy in its electric field or electrostatic field. It is a commonly used component in electrical and electronic circuits. It is mainly used in the field of electronics, power systems, communication, and computers. For example, capacitors are used in the rectifiers as filters and as tuning circuits in radio receivers.
A typical capacitor consists of two metallic plates separated by an insulator called a dielectric as shown in the following figure.
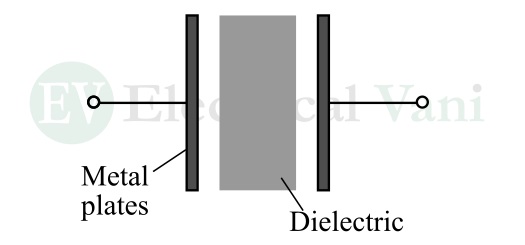
In practice, the plates are made up of aluminum foils and the dielectric can be air, paper, wax, mica, ceramic, etc.
Symbols of Capacitor
The symbols of capacitors are depicted in the following figure.

Charge Stored in Capacitor
When a source of voltage v is connected to the capacitor as shown in the following figure.

The voltage source deposits a positive electric charge +q on one plate while a negative electric charge -q on the other. In this condition, the capacitor is said to be charged.
The amount of charge stored in the capacitor is directly proportional to the applied voltage v i.e.,
$$q∝v$$
$$∴q=Cv$$
Where, C is a proportionality constant and is called the capacitance of the capacitor.
What is Capacitance?
Capacitance is the ability of a capacitor to store electric charge. It is defined as the ratio of the electric charge deposited on one plate of a capacitor to the voltage across the two plates i.e.,
$$C = \frac{q}{v}$$
However, the capacitance C of a capacitor is defined as the ratio of the electric charge q on one plate to the applied voltage v. But it does not depend on the charge q or voltage v.
Instead, the capacitance depends on the physical dimensions of the capacitor.
For example, the capacitance of a parallel plate capacitor is
- Directly proportional to the surface area of each plate.
- Directly proportional to the permittivity of the dielectric material placed between the plates.
- Inversely proportional to the distance between the plates.
Therefore, the capacitance of a parallel plate capacitor will be,
$$C=\frac{ϵA}{d}$$
Where, A is the surface area of each plate, d is the distance between the two plates, and ε is the permittivity of the dielectric.
Unit of Capacitance
The SI unit of capacitance is Farad and is denoted by F. It is given in honor of the English physicist Micheal Faraday.
$$\text{1 Farad}=\frac{\text{1 Coulomb}}{\text{Second}}$$
Factors Affecting Capacitance
In general, the following three factors affect the capacitance value of a capacitor:
- The surface area of each capacitor plate – the larger the surface area, the greater will be the capacitance of the capacitor.
- The distance or separation between the capacitor plates – the larger the distance between the plates, the lesser the capacitance.
- The nature or permittivity of the dielectric material – the higher the permittivity of the dielectric, the greater the capacitance of the capacitor.
Types of Capacitors
Capacitors are mainly classified into the following two types:
- Fixed Capacitors
- Variable Capacitors
A type of capacitor that has a constant value of capacitance that can never be changed at any time is called a fixed capacitor. Common examples of fixed capacitors are polyester capacitors, ceramic capacitors, electrolytic capacitors, mica capacitors, paper capacitors, etc.
A type of capacitor whose capacitance value can be adjusted within a certain range is known as a variable capacitor. Common examples of variable capacitors are tunning capacitors, trimmer capacitors, film-trim capacitors, etc.
Current-Voltage Relationship of Capacitor
As we know, the electric current is defined as,
$$i=\frac{dq}{dt}$$
For a capacitor, the charge is given by,
$$q = Cv$$
Differentiating on both sides, we get,
$$\frac{dq}{dt}=C \frac{dv}{dt}$$
$$∴i=C \frac{dv}{dt}$$
This equation is called the current-voltage relationship of a capacitor. A capacitor that satisfies this equation is called a linear capacitor.
If the capacitance of a capacitor is independent of the voltage i.e., linear capacitor, then the current-voltage relationship can be represented as a straight line passing through the origin as shown in the following figure.
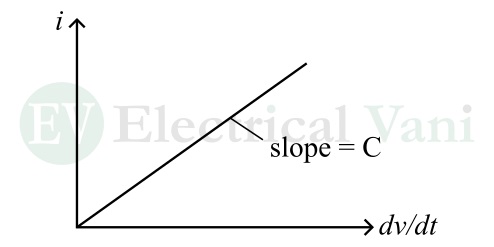
For a non-linear capacitor, the graph of the current-voltage relationship is not a straight line.
Voltage-Current Relationship of Capacitor
We can obtain the voltage-current relationship for a capacitor from the equation of the current-voltage relationship i.e.,
$$dv=\frac{1}{C} i dt$$
Integrating on both sides, we get,
$$⇒v(t)=\frac{1}{C} ∫_{-∞}^t i(τ) dτ$$
$$v(t)=\frac{1}{C} ∫_{t_0}^t i(τ) dτ + v(t_0 )$$
This equation is called the voltage-current relationship for a capacitor.
Where, v(t0) is the initial voltage across the capacitor and is given by,
$$v(t_0 )=\frac{q(t_0 )}{C}$$
Hence, from the voltage-current relationship of a capacitor, it is clear that the capacitor voltage depends on the past history of the charge stored in the capacitor. It proves that a capacitor has a memory.
Power and Energy of Capacitor
The instantaneous delivered to a capacitor is given by,
$$p = vi$$
Since, for a capacitor,
$$i=C \frac{dv}{dt}$$
Therefore, the instantaneous power is given by,
$$⇒p=Cv \frac{dv}{dt}$$
Now, the energy stored in the capacitor is given by,
$$w=∫_{-∞}^t p(τ) dτ =∫_{-∞}^t Cv \frac{dv}{dτ} dτ$$
$$⇒w=C∫_{-∞}^t v dv=C[\frac{v}{2}]_{-∞}^t$$
$$⇒w=\frac{1}{2} C[v(t)-v(-∞)]$$
Here, v(-∞) = 0 because the capacitor was initially uncharged.
$$∴w=\frac{1}{2} Cv^2$$
This equation represents the energy stored in a capacitor in the electric field between the plates.
It is important to note that we can retrieve this stored energy at a later time because an ideal or pure capacitor does not dissipate energy.
Important Points about Capacitor and Capacitance
The following are some important points to note about capacitor and capacitance:
(1). A fully charged capacitor acts as an open circuit to direct current (dc). Since, we know, the current through a capacitor is given by,
$$i=C \frac{dv}{dt}$$
If the applied voltage across the capacitor is constant or DC voltage, the current through the capacitor will be zero. Hence, a capacitor acts as an open circuit to dc.
(2). The voltage across a capacitor cannot change abruptly. If the voltage across a capacitor changes instantaneous i.e., in dt = 0, then,
$$i=C \frac{dv}{0}=∞$$
Which is practically impossible. Hence, a capacitor opposes an abrupt change in the voltage across it.
(3). An ideal capacitor does not dissipate energy. It stores energy in its electric field when charging and returns the stored energy to the circuit when discharging.
(4). A non-ideal practical capacitor has a certain resistance that acts in parallel with the capacitance as shown in the following figure.

The resistance is called the leakage resistance and it can be of the order of 100 MΩ. But in most practical applications, it can be neglected.
Conclusion
In conclusion, a capacitor is a passive circuit element used in electronic circuits to store energy in its electric field. The ability to store electrical energy is referred to as the capacitance of the capacitor. Capacitors are widely used in electrical and electronic circuits, communication, computer memories, and power systems. In this article, I have explained the concept of capacitors and capacitance in detail. If you have any questions related to the topic, kindly please let me know in the comment section, and I will answer shortly.