In this article, we will learn to determine the equivalent capacitance of capacitors in series and parallel. The capacitor is a passive circuit element used in electrical and electronic circuits to introduce the capacitive effect i.e., store electrical energy in an electrostatic field. In practical circuits, many capacitors are connected together to obtain a desired capacitance value. They are mainly combined in two configurations namely, series and parallel. When two or more capacitors are connected such that the same current flows through them, then, the capacitors are connected in series. When capacitors are connected such that the number of paths for current flow is equal to the number of capacitors, but the voltage across all the capacitors is the same, then it is called a parallel combination of capacitors.

Capacitors in Series
When two or more capacitors are connected end-to-end so that there is only a single path for the electrical current to flow, it is called a series combination of capacitors. A combination of N capacitors in series is shown in the following figure.
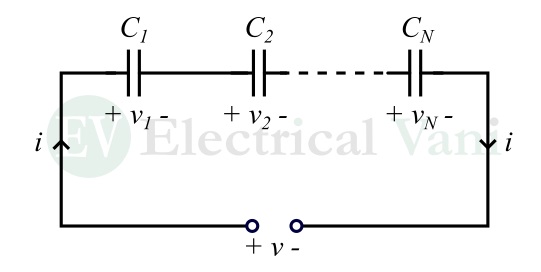
In this circuit, we will find the equivalent capacitance Ceq of the series-connected capacitor.
Here, we can observe that the same electric current i flows through all the capacitors in the series combination. Therefore, the charge on all capacitors is also the same.
Applying KVL to the loop, we can write,
$$v=v_1+v_2+⋯+v_N$$
For a capacitor, the voltage is given by,
$$v=\frac{1}{C} ∫_{t_0}^t i(τ)dτ+v(t_0 )$$
Therefore,
$$v=\frac{1}{C_1} ∫_{t_0}^t i(τ)dτ+v_1 (t_0 )+\frac{1}{C_2} ∫_{t_0}^t i(τ)dτ+v_2 (t_0 )+⋯+\frac{1}{C_N} ∫_{t_0}^t i(τ)dτ+v_N (t_0 )$$
$$⇒v=\left(\frac{1}{C_1} +\frac{1}{C_2} +⋯+\frac{1}{C_N}\right) ∫_{t_0}^t i(τ)dτ+v_1 (t_0 )+v_2 (t_0 )+⋯+v_N (t_0 )$$
$$⇒v=\frac{1}{C_{eq}} ∫_{t_0}^t i(τ)dτ+v(t_0 )$$
Hence,
$$\frac{1}{C_{eq}} =\frac{1}{C_1} +\frac{1}{C_2} +⋯+\frac{1}{C_N}$$
Thus, the equivalent capacitance of capacitors connected in series is equal to the reciprocal of the sum of the reciprocals of the capacitances of the individual capacitors.
The initial voltage v(t0) across the capacitor of equivalent capacitance is equal to the sum of initial voltage (at t0) across all capacitors i.e.,
$$ v(t_0 )=v_1 (t_0 )+v_2 (t_0 )+⋯+v_3 (t_0 )$$
Two Capacitors in Series
When two capacitors are connected in series, then their equivalent capacitance can be calculated as follows:
$$\frac{1}{C_{eq}} =\frac{1}{C_1} +\frac{1}{C_2} =\frac{(C_1+C_2)}{(C_1 C_2 )}$$
$$⇒C_{eq}=\frac{(C_1 C_2)}{(C_1+C_2 )}$$
Hence, the equivalent capacitance of two capacitors connected in series is equal to the product of both capacitances divided by their sum.
Capacitors in Parallel
When one end of each capacitor is connected to a common point and the other end of each capacitor is connected to another common point, and the number of paths for electric current to flow is equal to the number of capacitors, then it is called the parallel combination of capacitors.
Consider an electric circuit having N capacitors connected in parallel and across a source of v volts.
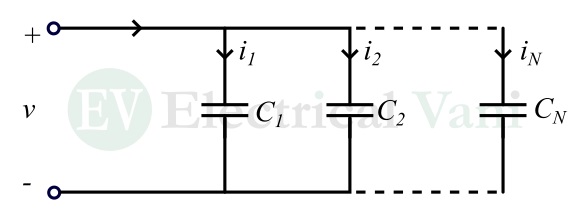
Here, the voltage across all capacitors is the same and equal to the supply voltage v. Applying KCL to the circuit, we can write,
$$i=i_1+i_2+⋯+i_N$$
For a capacitor, the capacitor current is given by,
$$i=C \frac{dv}{dt}$$
Therefore,
$$i=C_1 \frac{dv}{dt}+C_2 \frac{dv}{dt}+⋯+C_N \frac{dv}{dt}$$
$$⇒i=\left(C_1+C_2+⋯+C_N \right) \frac{dv}{dt}=C_{eq} \frac{dv}{dt}$$
Where,
$$C_{eq}=C_1+C_2+⋯+C_N$$
Hence, the equivalent capacitance of capacitors connected in parallel is equal to the sum of the individual capacitances.
Numerical Example – Find the equivalent capacitance of the circuit shown below.
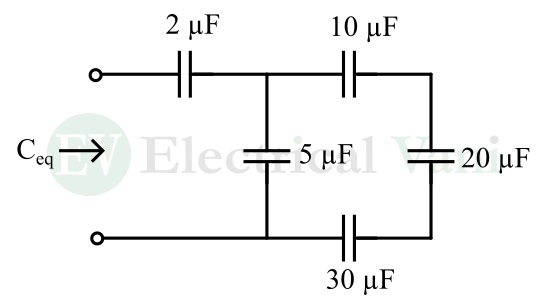
Solution – In this example, the capacitors 10µF, 20µF, and 30µF are in series, thus their equivalent capacitance is,
$$\frac{1}{C_{10-20-30}} =\frac{1}{10}+\frac{1}{20}+\frac{1}{30}=\frac{11}{60}$$
$$⇒C_{10-20-30}=\frac{60}{11}=5.45\text{ μF}$$
This 5.45 µF capacitor is in parallel with 5 µF, thus, their combined capacitance is,
$$C_{5.45-5}=5.45+5=10.45\text{ μF}$$
This 10.45 µF is in series with the 2 µF capacitor, thus the equivalent capacitance of the entire circuit is,
$$C_{eq}=\frac{(2×10.45)}{(2+10.45)}=1.68\text{ μF}$$
Conclusion
Hence, this is all about capacitors in series and parallel. In this article, we have studied about deriving formulas for the equivalent capacitance of a series combination of capacitors and a parallel combination of capacitors. Also, we have solved an example to understand the application of the formulae. Still, if you have any questions related to this topic, kindly please let me know in the comment section. I will answer shortly.