Half Adder Using NAND Gate – Learn How to Implement

In this article, I am going to explain how to implement the half adder using NAND gate only. In digital electronics, a half-adder is a digital arithmetic circuit made of logic gates that performs the addition of two binary digits. The NAND gate is a universal logic gate that can be used to realize any kind of logical function without the need for any other type of logic gate.

Before discussing the process of implementing half-adder using NAND gates only, let us first get an overview of half-adder and NAND gates individually.

What is NAND Gate?

In digital electronics. the NAND gate is a universal logic gate with two or more inputs and one output. The output of the NAND gate is logic 0 or low, only when all its inputs are logic 1 or high. For all other combinations of inputs, the output of the NAND gate is logic 1 or high.

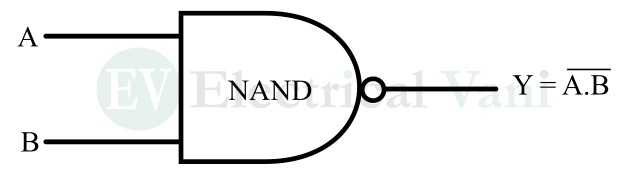
The operation of a two-input NAND gate is explained in the following truth table.

Inputs		Output
A	B	Y
0	0	1
0	1	1
1	0	1
1	1	0

The relationship between inputs and output of the NAND gate is described by its Boolean expression, which is given below.

$$Y=\overline{AB}$$

In this expression, the bar line over the product of inputs AB represents the inverted AND or NAND operation.

What is Half Adder?

In digital electronics, the half-adder is a digital arithmetic circuit used to perform the addition of two binary digits or bits.

It accepts two bits of a binary number at a time and produces a sum and a carry (if any) as the result.

It is called half-adder because this circuit is not capable of encountering the carry generated in the previous operation.

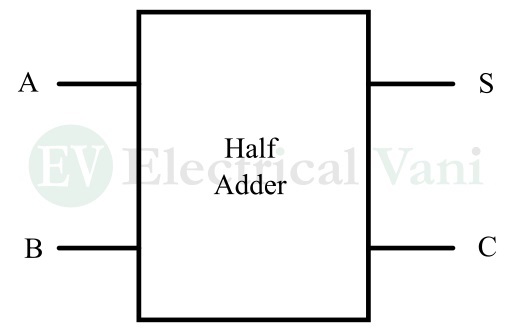
In the block diagram of the half-adder, the variables A and B are inputs, and S (Sum) and C (Carry) are outputs.

The operation of the half-adder circuit for different input combinations is given in the following truth table.

Inputs		Outputs
A	B	S	C
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

The relationship between the inputs and outputs of the half-adder is given by its Boolean expression.

The Boolean expression for the sum output of the half-adder is given below.

$$ S = A\overline{B}+\overline{A}B$$

$$⇒S=A⊕B$$

The Boolean expression for the carry output of the half-adder is given by,

C = A.B

Hence, this is all about NAND gate and half-adder in digital electronics. Let us now discuss how we can realize the half-adder using the NAND gate only.

Implement Half Adder using NAND Gate

To implement the half-adder using NAND gates, we have to derive the expression of the half-adder in terms of NAND gate logic. This is illustrated below.

The Boolean expression of the sum output of the half adder is given by,

$$S=A⊕B=A\overline{B}+\overline{A} B$$

Using Boolean laws, we get,

$$S=A\overline{B}+\overline{A} B+A\overline{A}+B\overline{B}$$

Since,

$$A\overline{A}=B\overline{B}=0$$

$$⇒S=A(\overline{A}+\overline{B})+B(\overline{A}+\overline{B})$$

$$⇒S=(A+B)(\overline{A}+\overline{B})$$

$$∵(\overline{A}+\overline{B})=\overline{A.B}$$

$$∴S=(A+B)(\overline{AB})$$

Using distribution law, we get,

$$S=A(\overline{AB})+B(\overline{AB})$$

Using the double complement rule, we get,

$$S=\overline{\overline{A(\overline{AB})+B(\overline{AB})}}$$

$$∴S=\overline{\overline{A(\overline{AB})}.\overline{B(\overline{AB})}}$$

This Boolean expression is equivalent to the sum output of the half-adder and it can be implemented using NAND gates only.

Let us now derive the Boolean expression for carry output in terms of NAND logic.

The carry output of the half-adder is given by,

C = A.B

Hence, using the double complement rule, we get,

$$C=\overline{\overline{AB}}$$

This is the equivalent Boolean expression of carry output in terms of NAND logic and it can be implemented using NAND gate only.

Let us now realize the circuit of the half-adder using NAND gates.

Circuit Diagram of Half-Adder using NAND Gates:

The circuit diagram of the half-adder using NAND gates is shown in the following figure.

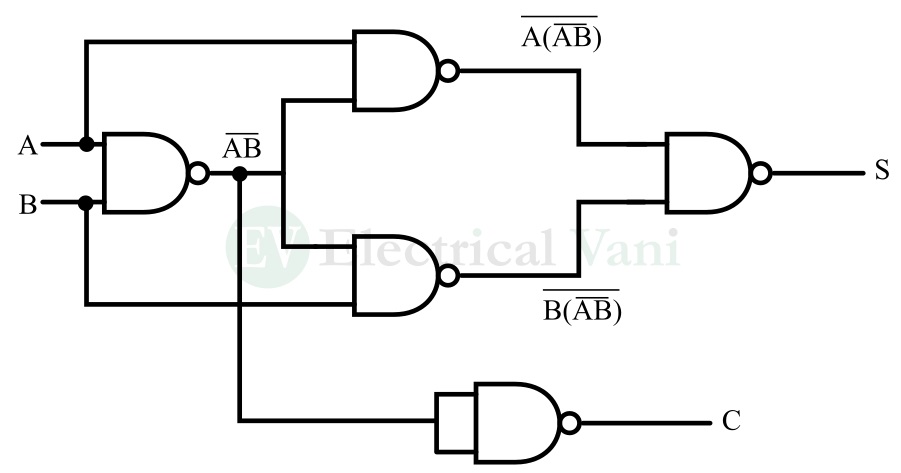
From this circuit, it can be seen that we can implement the half-adder circuit by using 5 NAND gates.

Conclusion

Hence, in this article, I have explained how to realize the half-adder circuit using the NAND gate. To implement the half-adder logic, we require 5 NAND gates and connect them as shown in the above figure.

If you have any queries related to this topic. Please let me know in the comment box. I will answer shortly.