Kirchhoff’s Voltage Law, also known as KVL, is a fundamental law used for analyzing a large variety of electric circuits. This law is also known as Kirchhoff’s second law. It was introduced by the German physicist Gustav Robert Kirchhoff in 1847. He also introduced another law known as Kirchhoff’s current law (KCL) which we have discussed in a separate article. Kirchhoff’s second law or KVL is based on the principle of conversion of energy which states that energy can neither be created nor destroyed, but can only be converted from one form to another.

Statement of Kirchhoff’s Voltage Law
Kirchhoff’s voltage law states that the algebraic sum of all voltage drops is equal to the algebraic sum of all EMFs around a closed loop in an electric circuit.
Mathematically,
$$∑\text{Voltage drops}=∑\text{EMFs}$$
In other words, the algebraic sum of voltage drops and EMFs around a closed loop is equal to zero i.e.,
$$∑\text{Voltage drops}+∑\text{EMFs}=0$$
For example, consider a closed loop in an electric circuit as shown in the following figure.
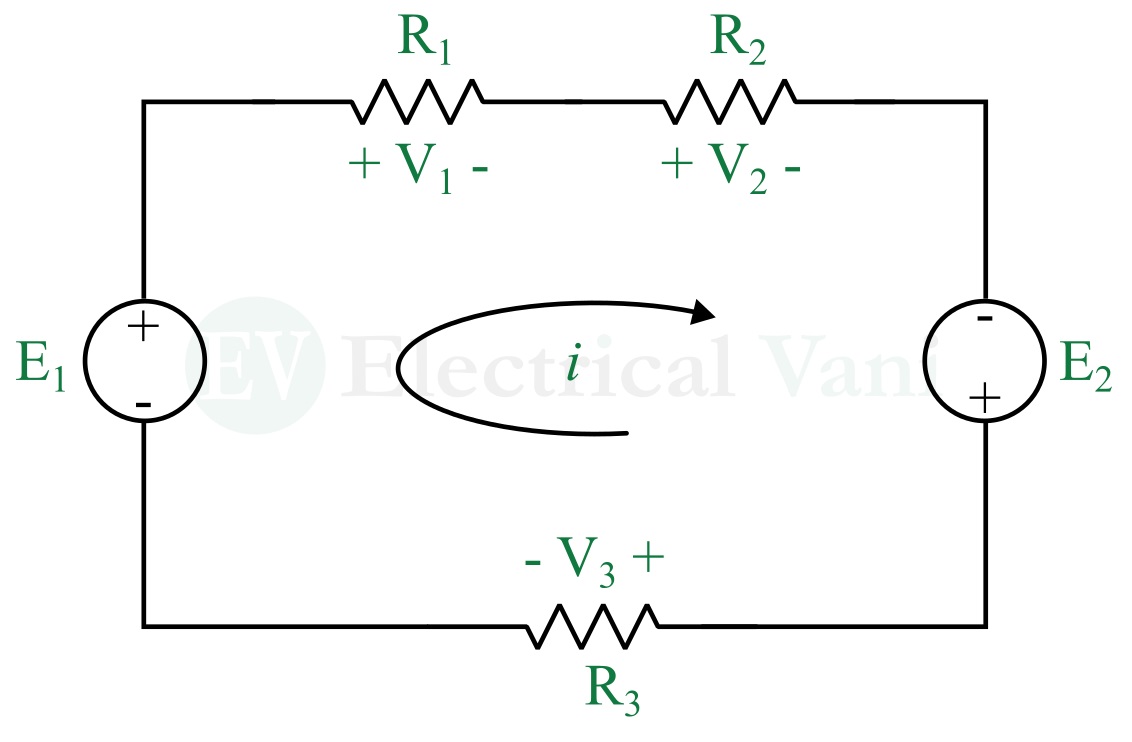
In this circuit, E1 and E2 are EMFs, and V1, V2, and V3 are voltage drops. Then, by applying KVL, we get the following equation,
$$E_1-V_1-V_2+E_2-V_3=0$$
$$⇒E_1+E_2=V_1+V_2+V_3$$
While writing the KVL equation for a loop, it is important to follow a proper sign convention. In general, the following two rules are used to write the KVL equations:
- We can start with any branch or element of the circuit and go around the loop or closed path either in a clockwise or anticlockwise direction and reach back to the starting point. A clockwise direction is mostly preferred.
- The sign taken on each voltage drop or EMF is the polarity of the next terminal encountered when we move around the loop.
In the above example, we started with the voltage source E1 and moved clockwise around the loop, then voltage drops and EMFs would be -V1, -V2, +E2, and -V3.
Important Points About KVL
The following are some important points about the Kirchhoff’s voltage law (KVL):
- KVL is based on the principle of conservation of energy, which states that the total energy within a closed electric circuit remains constant.
- In an electric circuit, a loop is a closed path that provides a path for current to flow.
- A mesh (most fundamental loop) is a closed path that does not contain any other loop inside it.
- In KVL, it is a convention that the EMFs or voltage rises are taken as positive, while the voltage drops are taken as negative.
- The sum of voltages around a loop or mesh is calculated algebraically, which means both the magnitude and polarity of the voltages are taken into account.
Combining Voltage Sources Using KVL
Kirchhoff’s Voltage Law (KVL) can be used to calculate the total voltage when multiple voltage sources are connected in series.
According to KVL, when a number of voltage sources are connected in series, the total voltage is the algebraic sum of the voltages of the individual voltage sources.
Let us understand this concept with the help of an example. Consider three voltage sources connected in series as shown below.
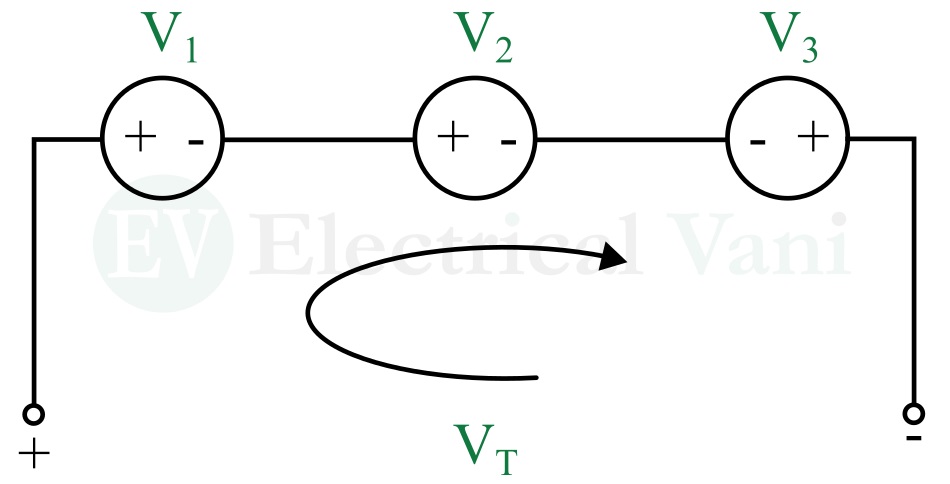
Applying KVL in the loop, we get,
$$V_T-V_1-V_2+V_3=0$$
$$∴V_T=V_1+V_2-V_3$$
It is important to note that we cannot combine two voltage sources of different voltages, say V1 and V2 in parallel unless V1 = V2. Otherwise, it will violate the KVL.
Examples Based on KVL
Example (1) – In the following circuit, find the voltages V1 and V2.
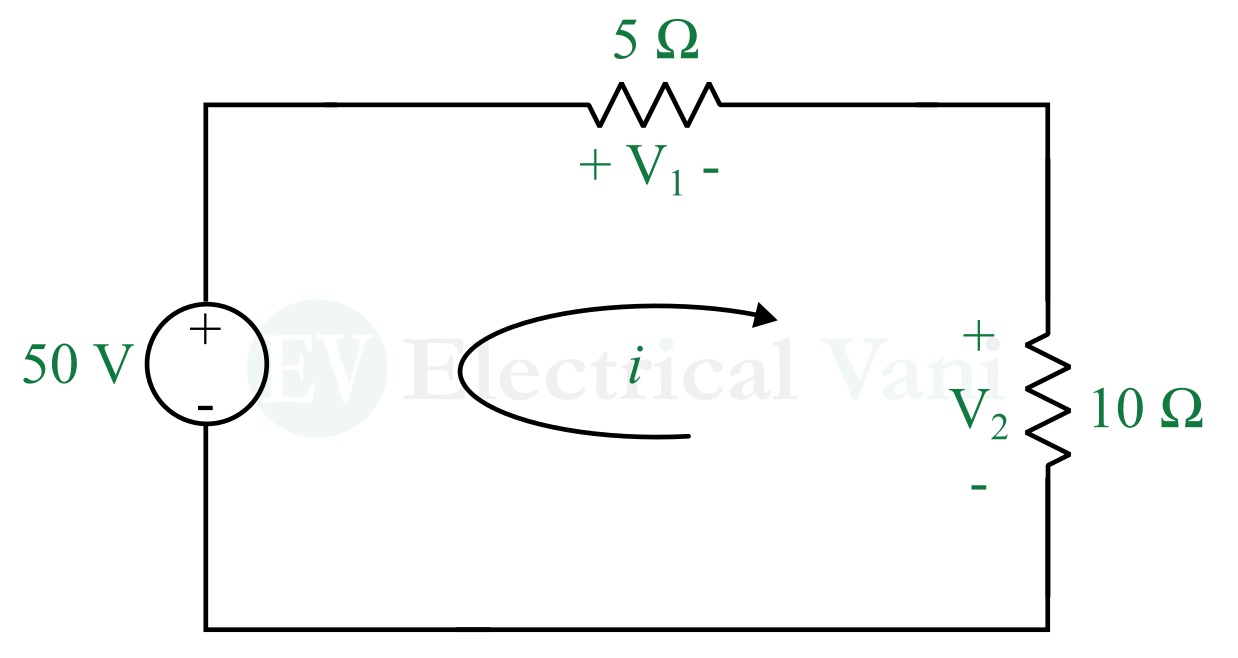
Solution – Applying KVL in the loop, we get,
$$50-V_1-V_2=0$$
By Ohm’s law, we have,
$$V_1=5i$$
$$V_2=10i$$
On substituting, we get,
$$50-5i-10i=0$$
$$15i=50$$
$$∴i=\frac{50}{15}=3.33\text{ A}$$
Hence, the voltages V1 and V2 will be,
$$V_1=5×3.33=16.65\text{ V}$$
$$V_2=10×3.33=33.3\text{ V}$$
Example (2) – Find the voltages V1 and V2 in the following circuit.
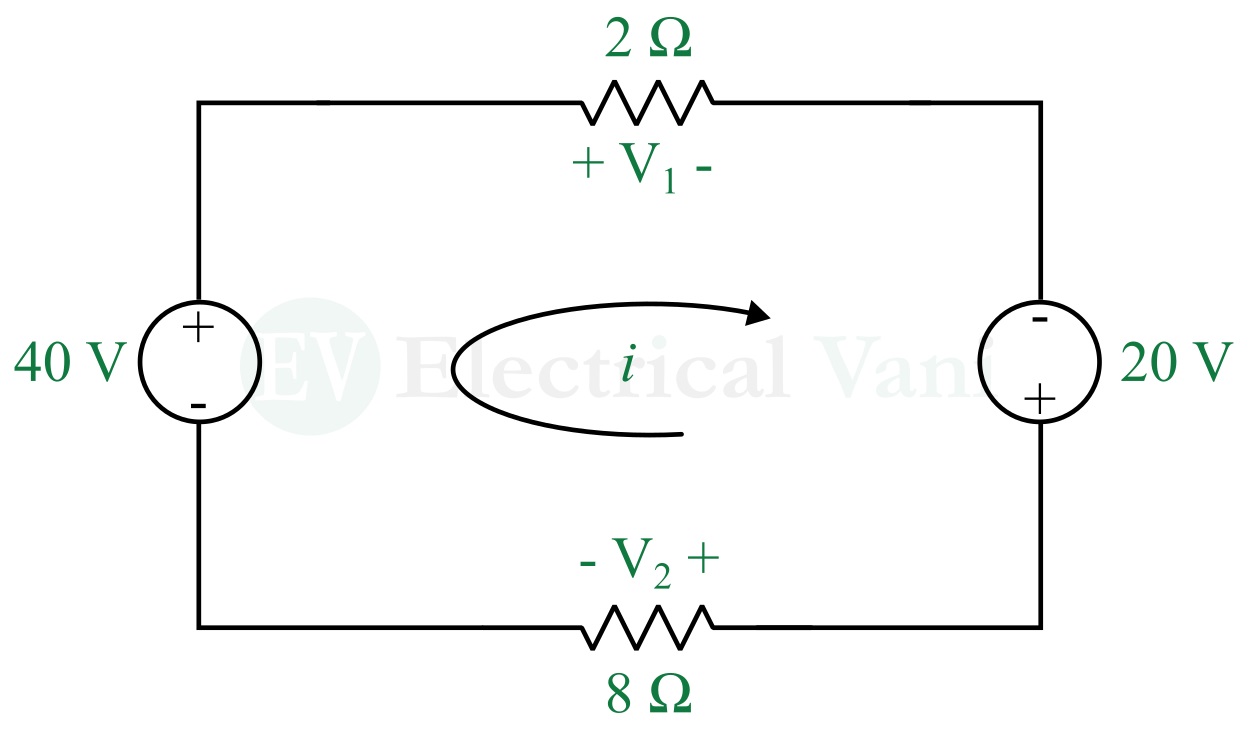
Solution – Applying KVL in the circuit, we get,
$$40-V_1+20-V_2=0$$
By Ohm’s law, we have,
$$V_1=2i$$
$$V_2=8i$$
On substituting,
$$40-2i+20-8i=0$$
$$⇒10i=60$$
$$∴i=\text{60}{10}=6\text{ A}$$
Then, the voltages V1 and V2 will be,
$$V_1=2×6=12\text{ V}$$
$$V_2=8×6=48\text{ V}$$
Problems Based on KVL
Try solving the following unsolved numerical problems to understand the application of KVL in circuit analysis.
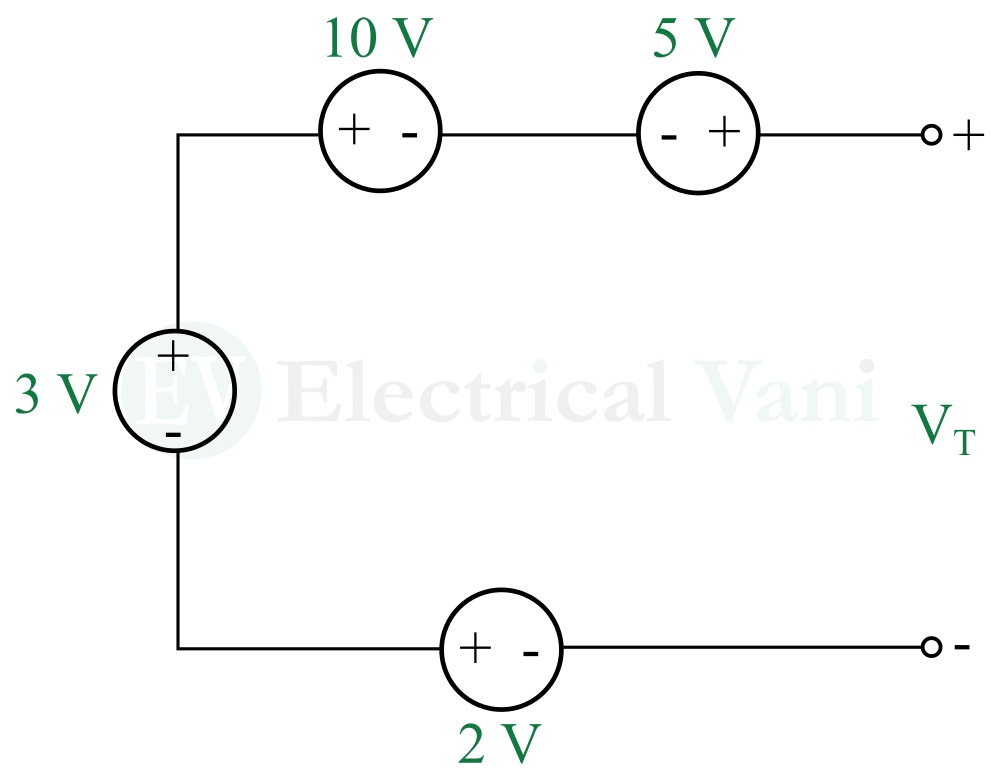
Problem (1) – Calculate the total voltage VT across the output terminal.
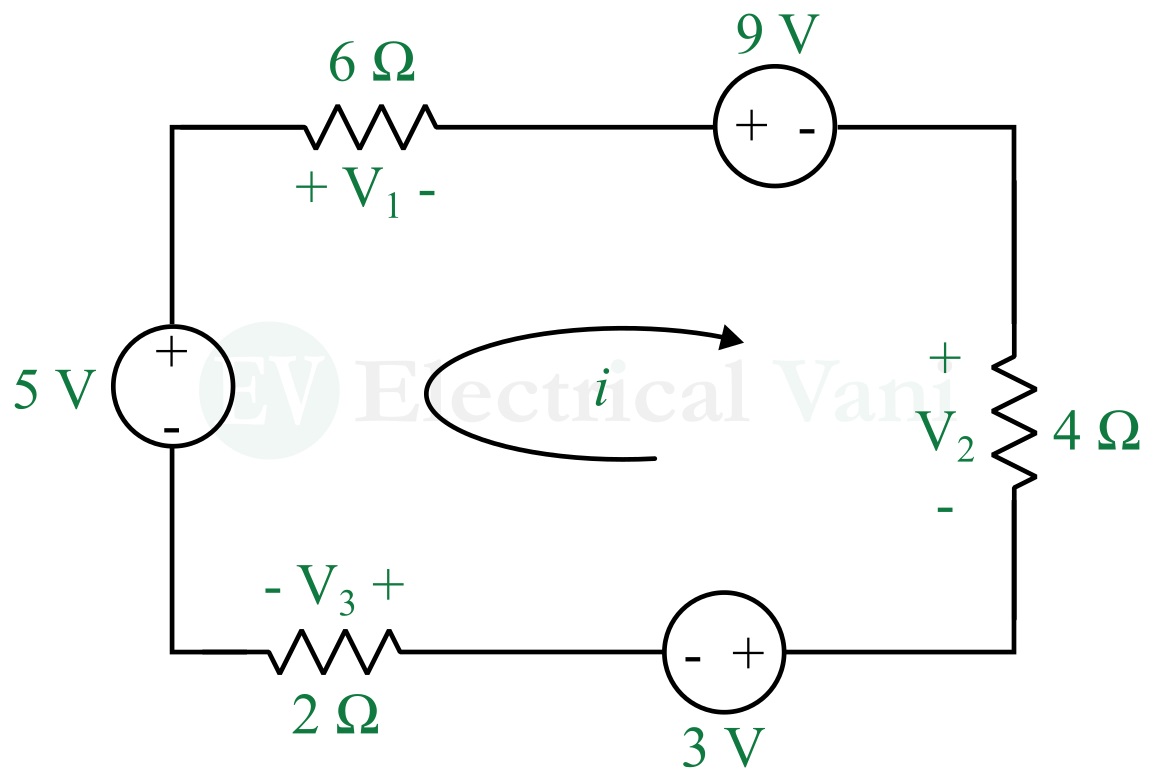
Problem (2) – Determine the voltages V1, V2, and V3 in the following circuit.
Conclusion
In this article, we have discussed Kirchhoff’s voltage and examples based on KVL. Still, if you have any questions related to this topic, kindly let me know in the comment section.