In this article, I will explain how to implement the OR gate using NAND Gate only. In digital electronics, the OR gate is a basic logic gate having two or more inputs and one output. The NAND gate is a type of universal logic gate, as it can be used to implement any kind of logic function without the need for any other type of logic gate. Therefore, we can utilize the NAND gates to realize the OR gate. In this article, we will study the step-by-step process to implement the OR gate using NAND gates only. But before that let us study the basics of OR gate and NAND gate individually.

What is OR Gate?
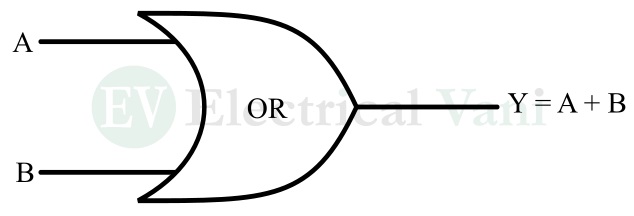
The OR gate is a logic gate in digital electronics that can have two or more inputs and one output. The output of the OR gate is logic 1 or high if any of the inputs is logic 1 or high. The output is logic 0 or low, if and only if all its inputs are logic 0 or low.
The operation of a two-input OR gate is explained in the following truth table.
|
Inputs |
Output |
|
|
A |
B |
Y |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
The relationship between the inputs and output of the OR gate is given by its Boolean expression, which is given below.
Y = A + B
Here, A and B are the input variables to the OR gate and Y is the output variable. The “+” denotes the OR operation.
Let us now get an overview of the NAND gate as well.
What is NAND Gate?
The NAND gate is a universal logic gate having two or more inputs and one output. It is called a universal logic gate, as it can be used to implement any kind of Boolean function without using any other kind of logic gate.
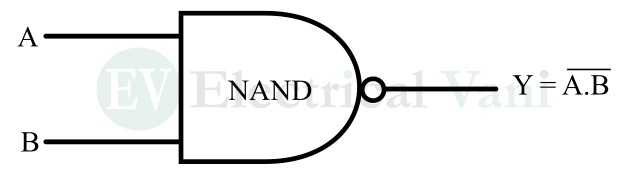
Basically, the NAND gate is a combination of two basic logic gates namely, AND gate and NOT gate. Hence, it is also known as NOTed-AND gate.
The output of the NAND gate is logic 0 or low, if and only if all the inputs are logic 1 or high. For all other input combinations, the output is logic 1 or higher.
The operation of a two-input NAND gate is given in the following truth table.
|
Inputs |
Output |
|
|
A |
B |
Y |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
The relationship between inputs and output of the NAND gate is given by a mathematical expression called Boolean expression of the NAND gate, which is given below.
$$Y = \overline{A.B}$$
Hence, this is all about the OR gate and NAND gate. Now, let us understand, how we can realize the OR gate using NAND gates.
Implement OR Gate using NAND Gate
To implement the OR gate using NAND gates, we have to derive the output expression of the OR gate in terms of the NAND gate. This is explained here.
The desired output is,
Y = A + B
According to the double complement rule, we can write,
$$Y = \overline{\overline{A + B}}$$
$$Y = \overline{\overline{A} .\overline{B}}$$
This expression is equivalent to OR gate output and can be realized using NAND gates only.
Circuit Diagram of OR Gate using NAND Gate:
The following figure depicts the circuit diagram of the OR gate using the NAND gate.
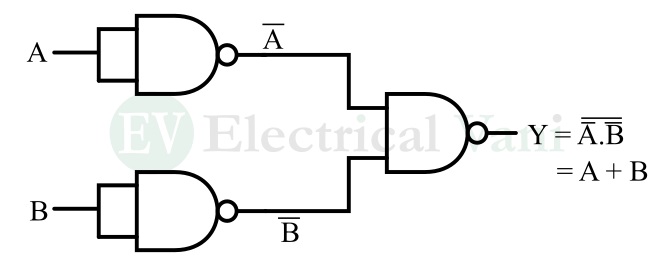
From this figure, it is clear that the implementation of OR gate using NAND gates requires only three NAND gates.
In this circuit, the first two NAND gates act as inverters to produce a complement of input variables, and the third NAND gate produces the output function equivalent to the OR gate.
Conclusion
In this article, we have studied how to implement the OR gate using NAND gates only. In conclusion, the NAND gate is a universal logic gate, hence it can be used to realize the OR operation. To implement the OR operation, we require three NAND gates connected together as described in the above section of this article.
If you have any queries related to this topic, please let me know in the comment section. I will answer shortly.