Nodal analysis is a general method of analyzing electrical circuits. This method involves the use of node voltages as the circuit variables. The use of node voltages instead of element voltages significantly reduces the number of simultaneous equations and makes the analysis convenient. In nodal analysis, we focus on finding the node voltages and then we use these node voltages in solving the circuits.

There are following two types of nodal analysis frequently used in circuit analysis:
- Nodal Analysis without Voltage Sources
- Nodal Analysis with Voltage Sources
How to Determine Node Voltages?
Consider an electric circuit with “n” nodes, then we follow the steps given below to determine the node voltages:
Step (1) – Select one of the nodes as a reference (ground) node.
Step (2) – Assign voltages like V1, V2, V3, …, and Vn-1 to all the non-reference nodes with respect to the reference node.
Step (3) – Apply KCL (Kirchhoff’s Curren Law) to each of the non-reference nodes. Then, use Ohm’s law to determine the branch current equations in terms of node voltages.
Step (4) – Solve the simultaneous equations to obtain the node voltages and hence other circuit parameters.
Important Concepts Related to Nodal Analysis
The following are some important concepts that are related to nodal analysis.
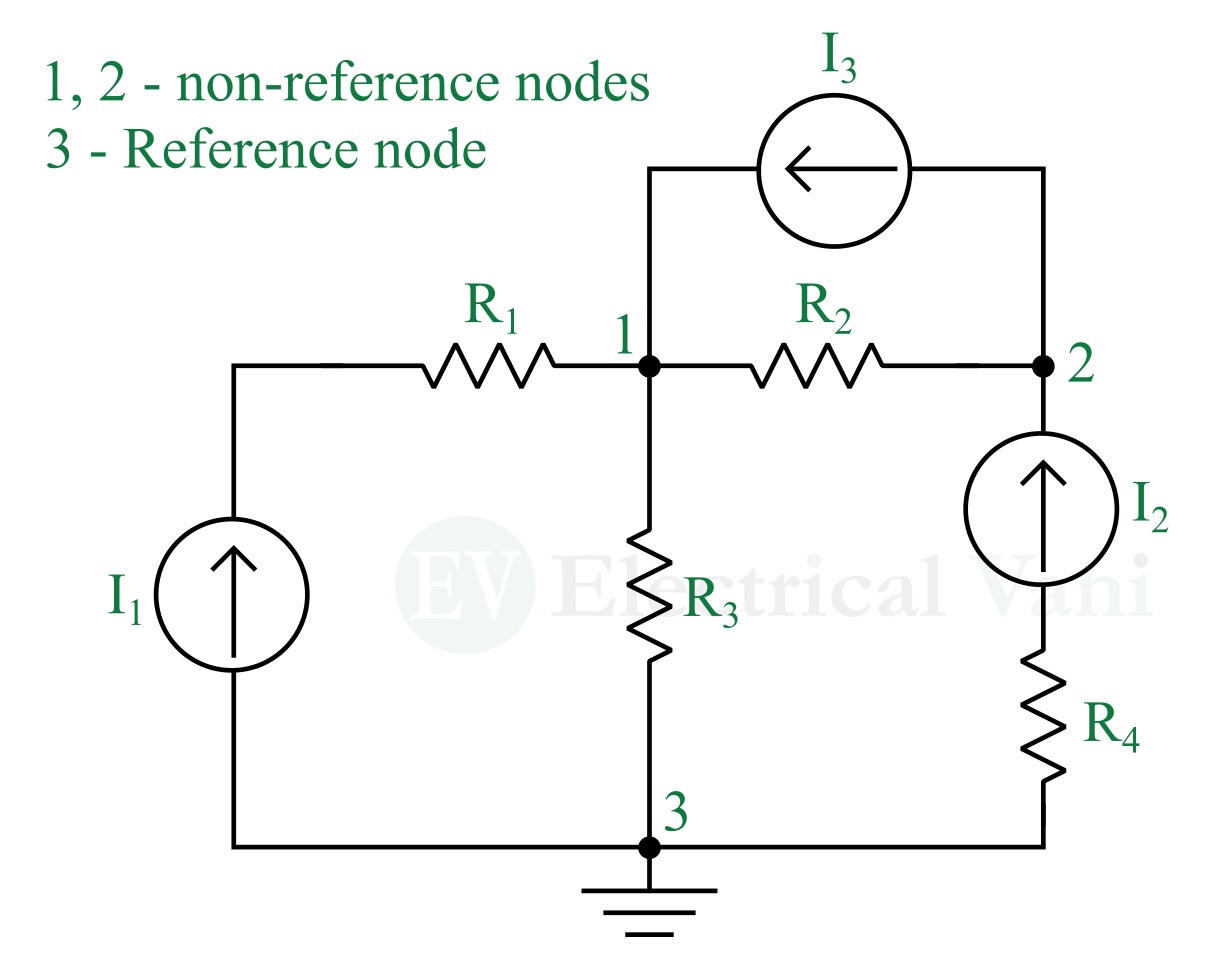
- In nodal analysis, the reference node, also known as the datum node, is a common node taken as a reference point with respect to all other nodes. It is commonly the ground node because it is assumed to have zero potential.
- In nodal analysis, current flows from a higher potential to a lower potential in a passive circuit element like a resistor.
- In nodal analysis, a non-reference node (also called a junction) is a node to which three or more branches are connected.
The following figure highlights the non-reference nodes and reference nodes.
Nodal Analysis without Voltage Sources
In this section, we will learn to use nodal analysis to solve an electric circuit having no voltage sources.
Consider an electric circuit having current sources and resistors as shown in the following figure.
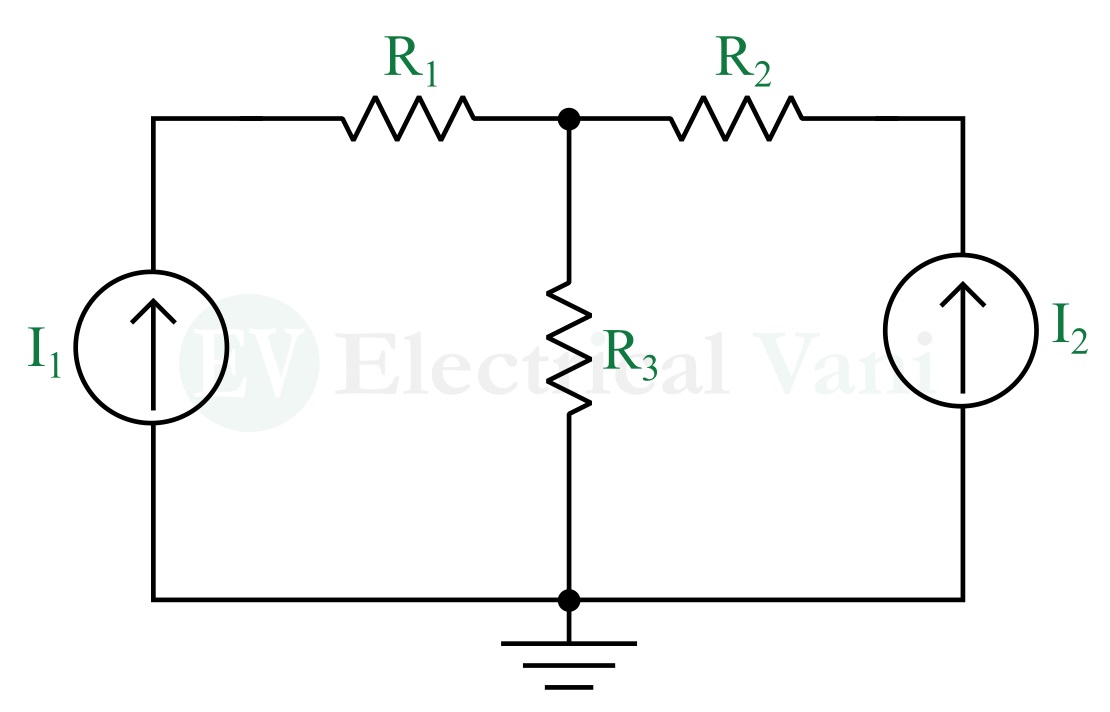
We solve this circuit as per the following steps:
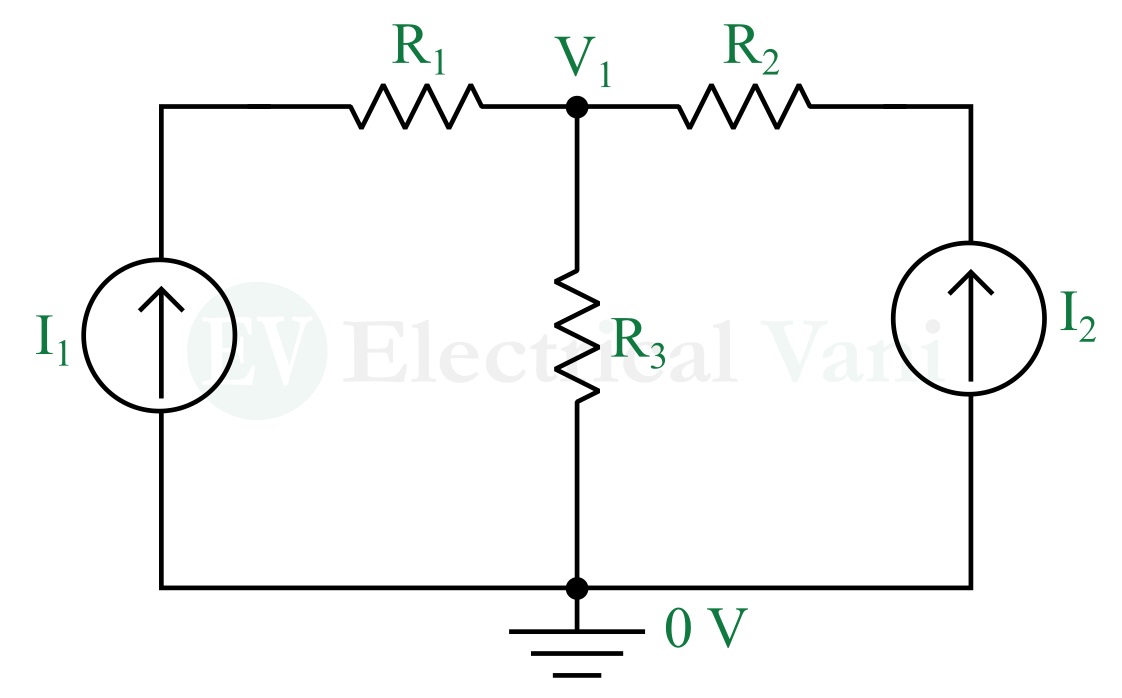
Step (1) – Selecting a reference/ground node and assuming it to have 0 V potential and assigning voltages to all other non-reference nodes. In this circuit, there is only one non-reference node and we assigned V1 as node voltage to it.
Step (2) – We apply KCL to the non-reference node in the circuit. We consider I1, I2, and I3 currents flowing through resistors R1, R2, and R3 respectively as shown in the following figure.
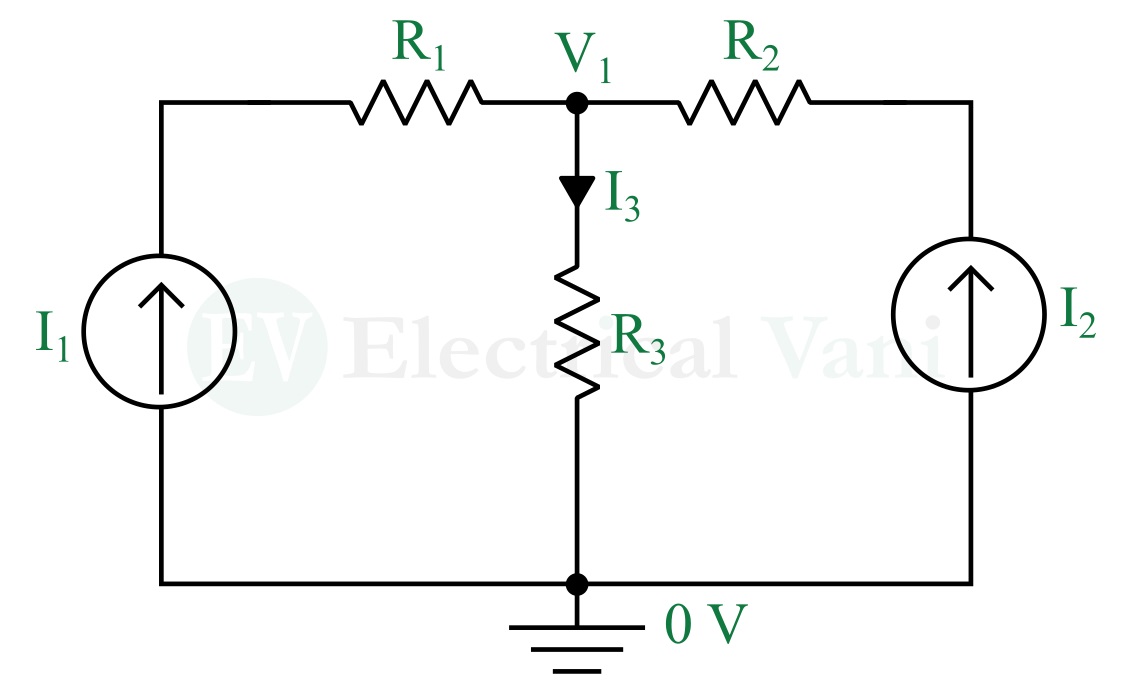
Hence, KCL gives,
$$I_1+I_2=I_3$$
Now, we apply Ohm’s law to express the currents I1, I2, and I3 in terms of node voltages as follows,
$$I_1=\frac{0 – V_1}{R_1} =\frac{-V_1}{R_1}$$
$$I_2=\frac{0-V_1}{R_2} =\frac{-V_1}{R_2}$$
$$I_3=\frac{V_1-0}{R_3} =\frac{V_1}{R_3}$$
Therefore,
$$\frac{-V_1}{R_1} -\frac{V_1}{R_2} =\frac{V_1}{R_3}$$
Step (3) – Finally, we solve this equation to obtain the value of voltage V1.
Let us now consider a solved example to understand the above procedure of nodal analysis.
Example – Determine the node voltages and branch currents in the circuit shown in the following figure.
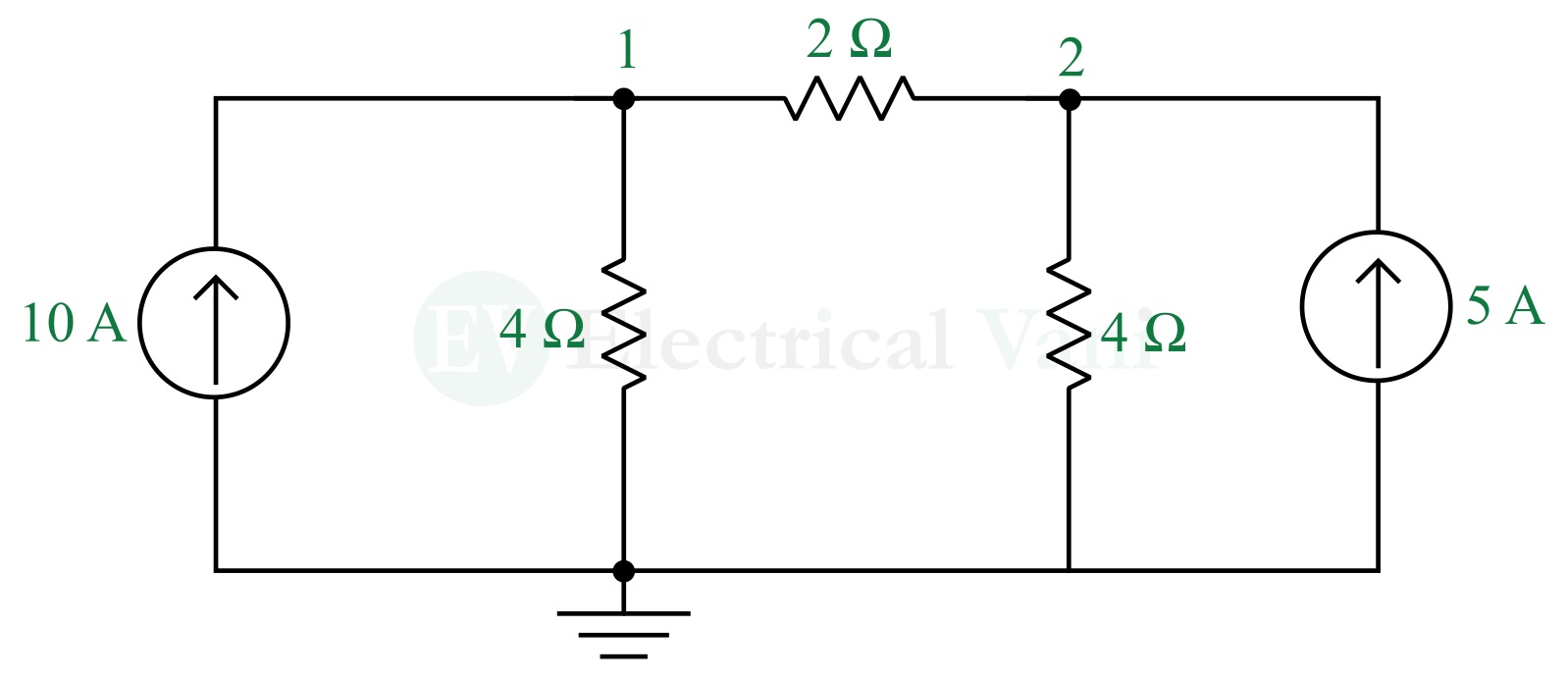
Solution – Redrawing the circuit with the node voltages, reference node, and branch currents.
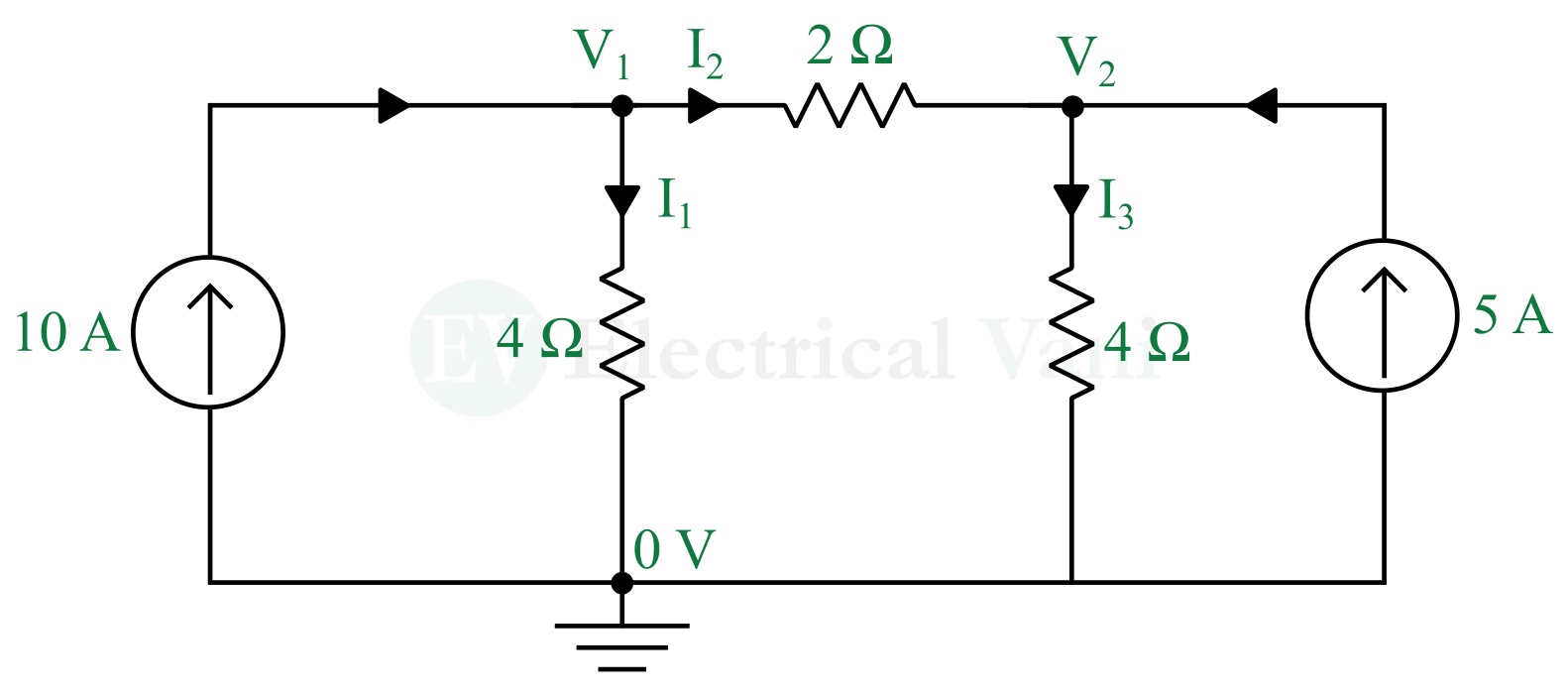
At node-1, applying KCL and Ohm’s law, we get,
$$10=I_1+I_2$$
$$⇒10=\frac{V_1}{4}+\frac{V_1-V_2}{2}$$
$$3V_1-2V_2=40…(1)$$
At node-2, applying KCL and Ohm’s law, we get,
$$5+I_2=I_3$$
$$⇒5+\frac{V_1-V_2}{2}=\frac{V_2}{4}$$
$$-2V_1+3V_2=20…(2)$$
Now, we have simultaneous equations (1) and (2), and we will solve these two equations to determine the value of node voltages V1 and V2. For this, we can use any method.
On solving equations (1) and (2), we get,
$$V_1=32\text{ V}$$
$$V_2=28\text{ V}$$
The branch currents will be,
$$I_1=\frac{V_1}{4}=\frac{32}{4}=8\text{ A}$$
$$I_2=\frac{V_1-V_2}{2}=\frac{32-28}{2}=2\text{ A}$$
$$I_3=\frac{V_2}{4}=\frac{28}{4}=7\text{ A}$$
Nodal Analysis with Voltage Sources
Now, we will understand the nodal analysis of circuits containing voltage sources.
There could be the following two cases:
Case I – When a voltage source is connected between a reference node and a non-reference node. Then, the voltage at the non-reference node is set equal to the voltage of the voltage source.
For example, In the following figure, a 20 V voltage source is directly connected to the node-1. Thus, the node voltage V1 will be equal to 20 V.
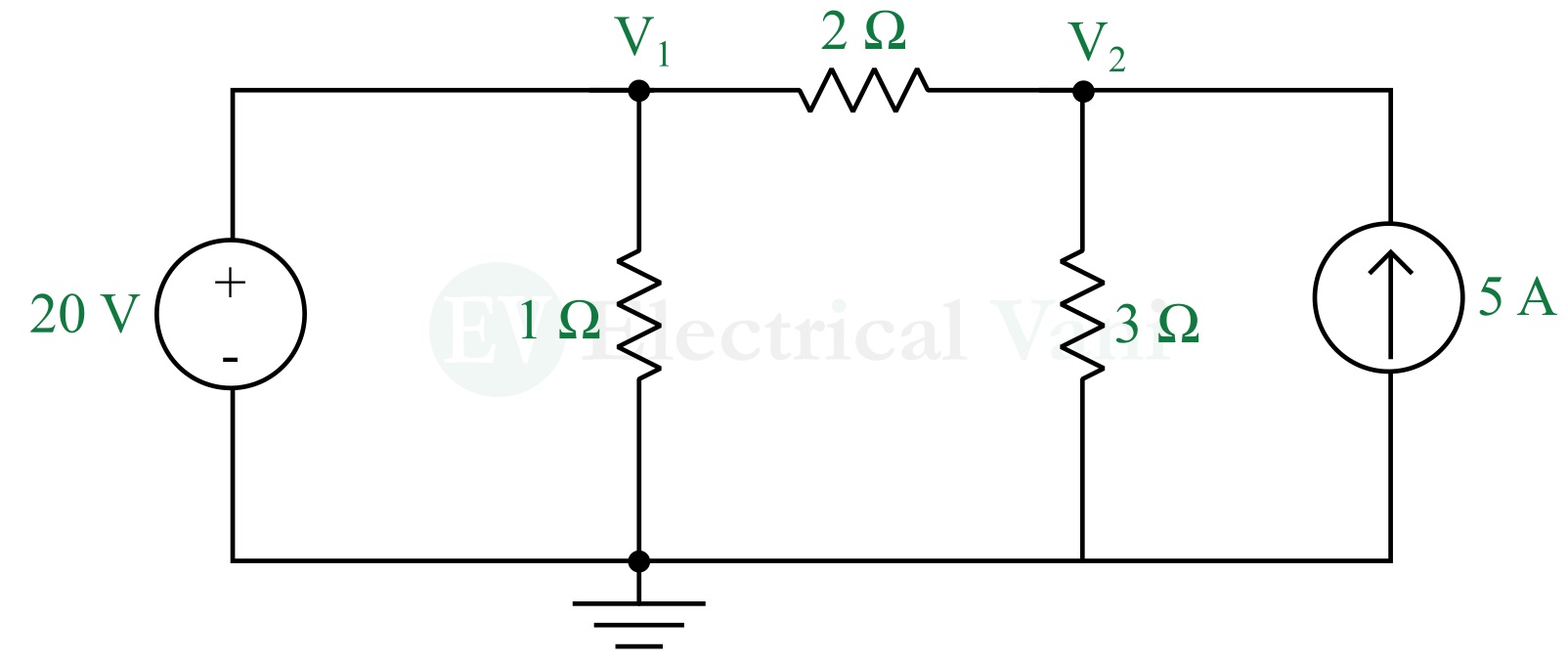
Solving the case-I circuits is similar to the previous one i.e., as nodal analysis without voltage sources.
Case II – When a voltage source, either dependent or independent, is connected between two non-reference nodes, then the two non-reference nodes form a supernode as shown in the following figure.
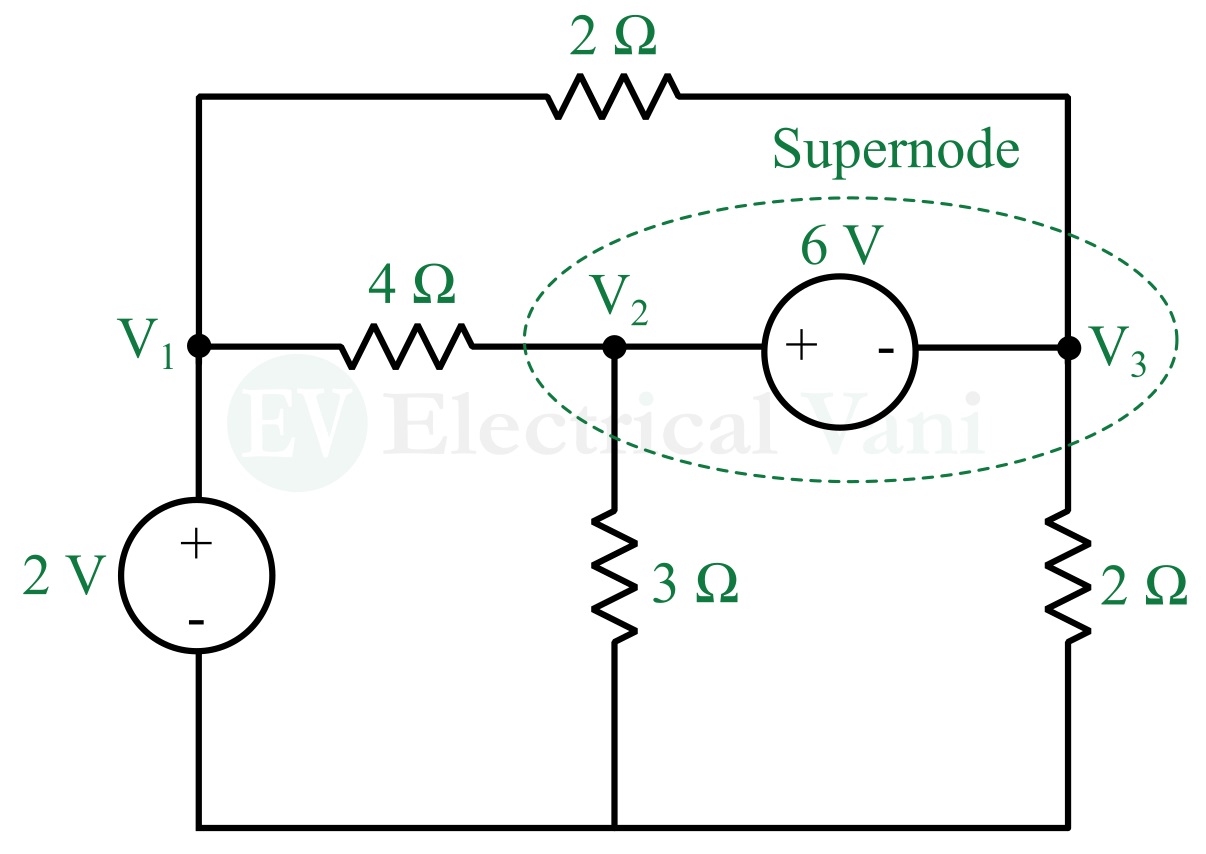
A supernode is a common node formed by enclosing a voltage source connected between two non-reference nodes and any circuit element connected in parallel with it.
To determine the node voltage of the supernode, both KCL and KVL are used simultaneously.
Solving the circuits having a supernode is slightly different from the previous solution. Let us understand this with the help of an example.
Example – Find the node voltages and branch currents in the following circuit.
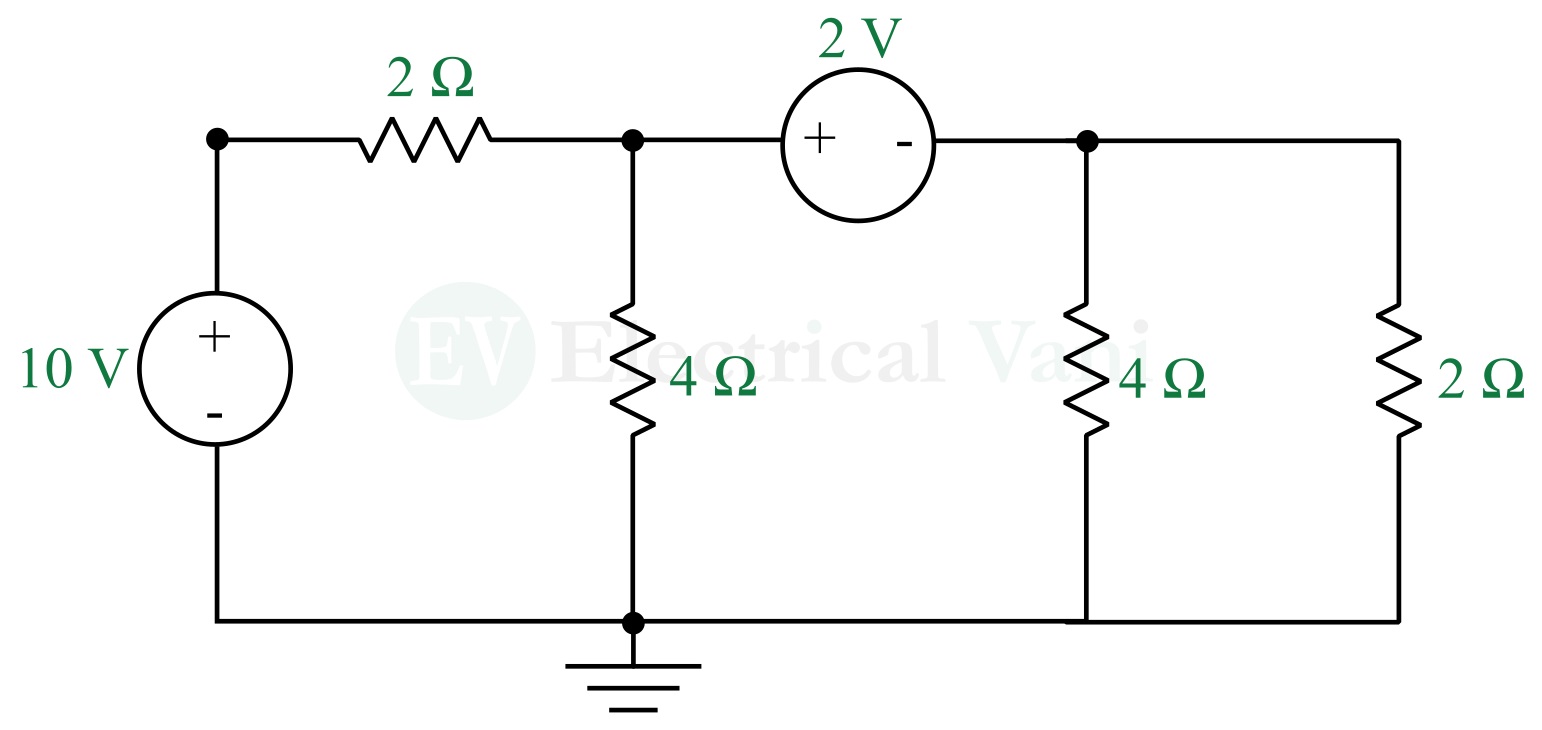
Solution – Redrawing the circuit with node voltages, supernode, reference node, and branch currents as shown in the following figure.
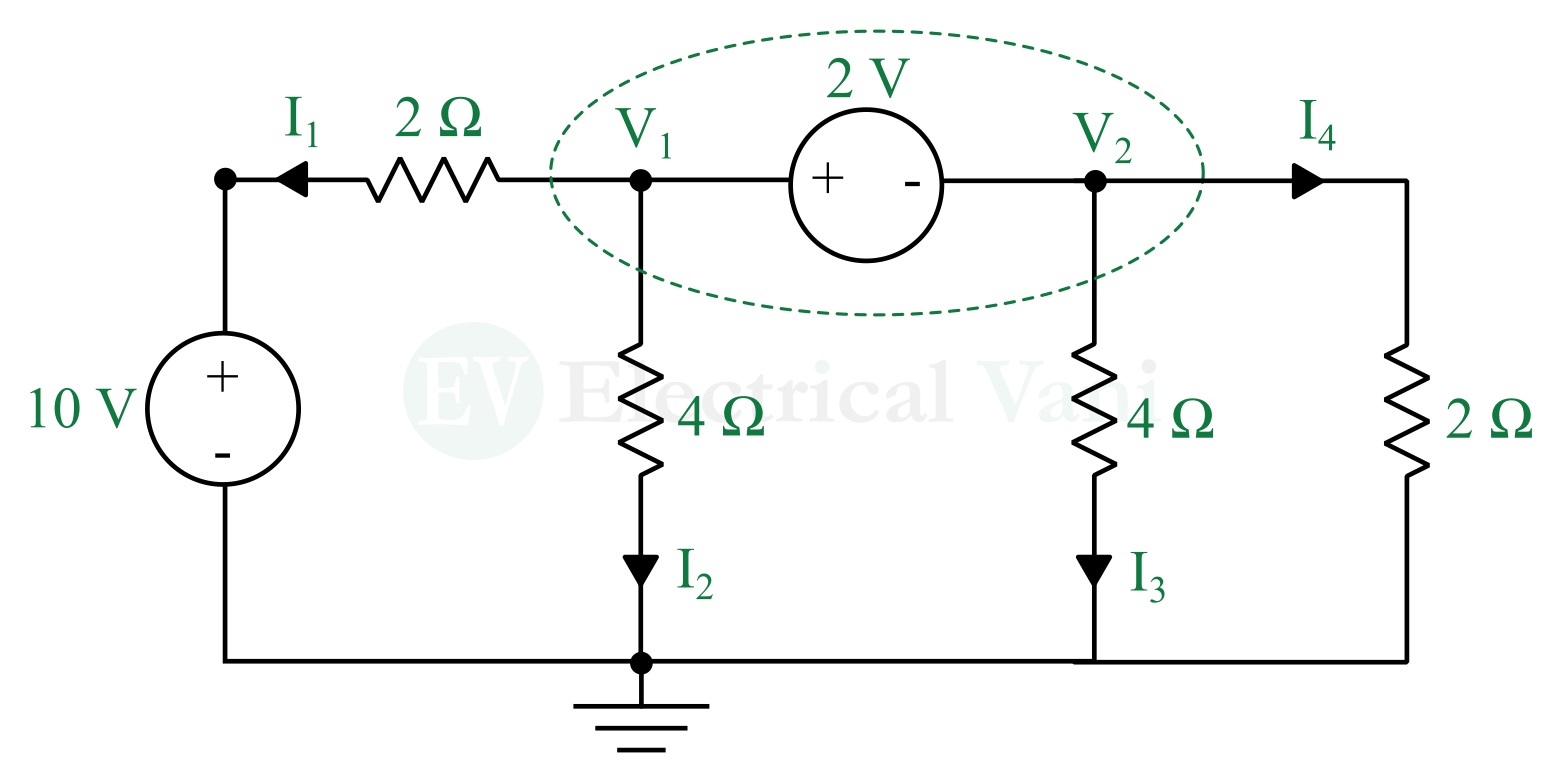
Applying KCL to the supernode, we get,
$$I_1+I_2+I_3+I_4=0$$
Using Ohm’s law, we get,
$$\frac{V_1-10}{2}+\frac{V_1}{4}+\frac{V_2}{4}+\frac{V_2}{2}=0$$
$$⇒\frac{2V_1-20+V_1+V_2+2V_2}{4}=0$$
$$⇒3V_1+3V_2=20…(1)$$
To get the relationship between node voltages V1 and V2, we apply KVL at nodes 1 and 2, we get,
$$V_1-2-V_2=0$$
$$⇒V_1=2+V_2…(2)$$
From equations (1) and (2), we get,
$$3(2+V_2 )+3V_2=20$$
$$6+3V_2+3V_2=20$$
$$⇒V_2=2.33\text{ V}$$
Therefore,
$$V_1=2+2.33=4.33\text{ V}$$
Now, the branch currents will be,
$$I_1=\frac{V_1-10}{2}=\frac{4.33-10}{2}=-2.835\text{ A}$$
$$I_2=\frac{V_1}{4}=\frac{4.33}{4}=1.083\text{ A}$$
$$I_3=\frac{V_2}{4}=\frac{2.33}{4}=0.583\text{ A}$$
$$I_4=\frac{V_2}{2}=\frac{2.33}{2}=1.165\text{ A}$$
You can try solving numerical examples based on nodal analysis from reference books or previous year papers of various technical competitive examinations like GATE.
Conclusion
This is all about nodal analysis with/without voltage sources. This article completely explains the concept of nodal analysis with the help of examples. If you have any queries related to this topic, kindly let me know in the comment section.