If you were searching about how to implement XOR Gate using NOR Gate, then this article is for you. In this article, I will explain the complete step-by-step guide to implementing the XOR gate using NOR Gate. Both XOR gates and NOR gates are widely used logic gates in digital electronics. The XOR gate is a type of derived logic gate which performs exclusive OR operation. Whereas the NOR gate is a type of universal logic gate that performs Noted OR operation. Since the NOR gate is a universal logic gate, it can be used to implement any kind of logic function without the need for any other logic gate.

This article is meant to explain the implementation of the XOR gate using the NOR gate. Before that let’s have a look into the XOR gate and NOR gate individually.
What is XOR Gate?
XOR gate, also called Ex-OR gate or Exclusive OR gate, is a two-input and one-output logic gate whose output is in logic 1 or high state, only when both inputs are dissimilar i.e., one is high and the other is low.
The Boolean function of the XOR gate is given below,
$$Y=A\overline{B}+\overline{A} B=A⊕B$$
Here, A and B are input variables and Y is the output variable.
What is NOR Gate?
NOR gate is a combination of two basic logic gates namely, OR gate and NOT gate. It is basically the OR gate followed by a NOT gate.
The NOR gate is a type of universal logic gate, as it can be used to implement any kind of logical function without using any other type of logic gate.
The NOR gate can have two or more inputs, but only one output. The output of the NOR gate is logic 1 or high only when all its inputs are logic 0 or low.
The Boolean expression of the NOR gate is given below:
$$Y = \overline{A+B}$$
Here, A and B are the input variables and Y is the output variable.
After getting a brief overview of the XOR gate and NOR gate, let us now learn how to implement the XOR gate using NOR gate only.
Implement XOR Gate using NOR Gate
When we want to implement an XOR gate using a NOR gate, we basically try to obtain the Boolean expression of the XOR gate from a logic circuit consisting of NOR gates.
Hence, to implement the XOR gate using the NOR gate, we have to establish a relationship between Boolean expressions of XOR and NOR gates.
The following mathematical derivation explains how we can obtain the output of the XOR gate from a logic circuit made up of NOR gates only.
The output of the XOR gate is given by,
$$Y=\overline{A}B+A\overline{B}=A⊕B$$
Taking the double complement on the right-hand side, we get,
$$Y=\overline{\overline{A⊕B}}=\overline{A⊙B}$$
$$⇒Y=\overline{AB+\overline{A}.\overline{B}}$$
$$⇒Y=\overline{AB+(\overline{A+B})}$$
$$⇒Y=\overline{\overline{\overline{AB}}+\overline{(A+B)}}$$
$$⇒Y=\overline{\overline{(\overline{A}+\overline{B})}+\overline{(A+B)}}$$
Hence, this Boolean expression is equivalent to the output of the XOR gate and it can be implemented using NOR gates only.
Let us now implement this Boolean expression using NOR gates.
XOR Gate using NOR Gate Circuit Diagram
The following circuit diagram demonstrates the implementation of the XOR gate using NOR gates only. This implementation is done as per the above-performed computation.
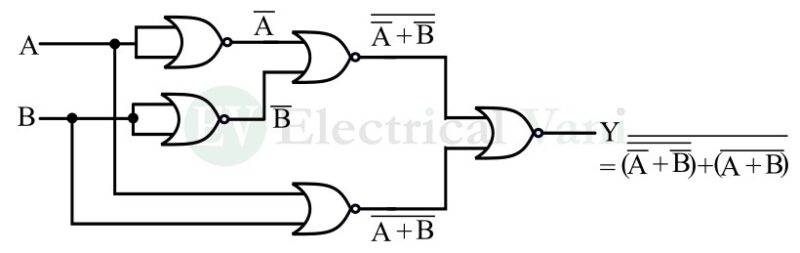
From this circuit diagram of the XOR gate using the NOR gate, it is clear that it requires six NOR gates.
Conclusion
Hence, in this article, we have studied how to implement the XOR gate using the NOR gate. In conclusion, the implementation of the XOR gate requires six NOR gates. NOR gate is a universal logic gate hence it can be used to implement the XOR operation, as described in this article.
If you have any queries on this topic, please let me know in the comment section.