In this article, we will learn about mesh analysis, its theoretical explanation, and solved examples. As we know, for circuit analysis, there are various tools available such as Ohm’s law, KCL, KVL, and nodal analysis. Similarly, mesh analysis is a method of circuit analysis that is based on Kirchhoff’s second law called KVL (Kirchhoff’s Voltage Law). In mesh analysis, electric circuits are analyzed using mesh currents as the circuit variables. In other words, mesh analysis allows us to analyze electric circuits by writing circuit equations in terms of mesh currents and then these equations are solved to obtain the circuit parameters.

What is a Mesh?
Before going to discuss mesh analysis, it is important to understand what is a mesh in an electric circuit.
So, a mesh is nothing but a loop that cannot subdivided into other loops. Hence, in an electric circuit, the most elementary loop which does not contain any other loop within it, is called a mesh.
Also, a loop in an electric circuit is a closed path through which an electric current can flow.
Important Points About Mesh Analysis
The following points are of much importance while dealing with mesh analysis:
- In mesh analysis, Kirchhoff’s voltage law (KVL) is utilized to determine the unknown mesh currents.
- Mesh analysis can be applied to planner circuits only, and it is not applicable to a non-planner circuit.
- A planner circuit is an electric circuit that can be drawn in a plane with no branches crossing one another.
- A circuit is said to be a non-planner circuit if there is no way to draw it to avoid the branches crossing each other.
Steps Involved in Mesh Analysis
The following steps are to be followed to apply mesh analysis to an electric circuit
Step (1) – Identify meshes in the circuit and assign currents to them.
Step (2) – Apply KVL and Ohm’s law to write mesh equations in terms of mesh currents.
Step (3) – Solve the mesh equations simultaneously to obtain the mesh currents.
Let us understand these steps with the help of an example.
Consider an electric circuit shown in the following figure.
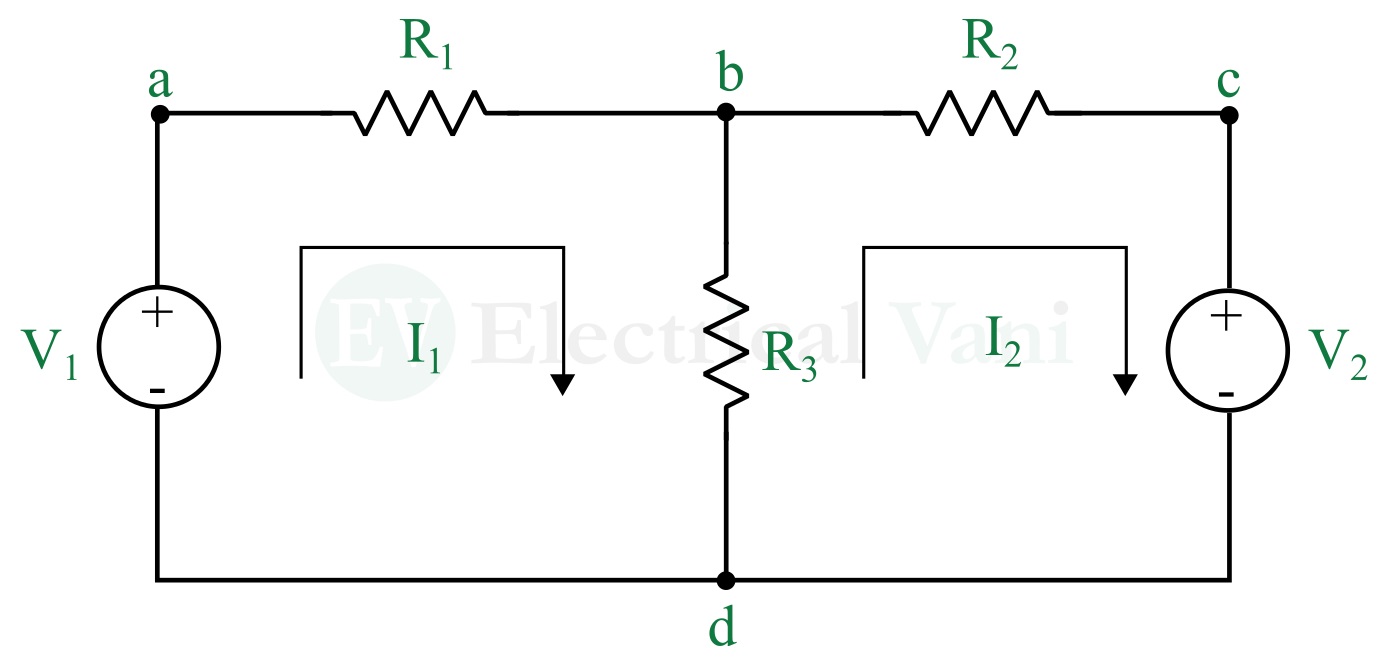
In this circuit, there are two meshes namely, abda and bcdb. We assigned I1 and I2 as the mesh currents to these two meshes. In general, we take the clockwise direction of currents.
Now, we apply KVL to each mesh, we get the following expressions.
Applying KVL to mesh-1, we get,
$$V_1-I_1 R_1-(I_1-I_2 ) R_3=0$$
$$V_1=I_1 (R_1+R_3 )-I_2 R_3…(1)$$
Applying KVL to mesh-2, we get,
$$-I_2 R_2-V_2-(I_2-I_1 ) R_3=0$$
$$V_2=-I_2 R_2-I_2 R_3+I_1 R_3$$
$$V_2=I_1 R_3-I_2 (R_2+R_3 )…(2)$$
Finally, we solve these equations simultaneously to obtain the values of currents I1 and I2.
Let us take a solved numerical example to understand the circuit solution using mesh analysis.
Numerical Example – Find the mesh currents in the following circuit.

Solution – Assigning mesh currents and applying KVL to the circuit.
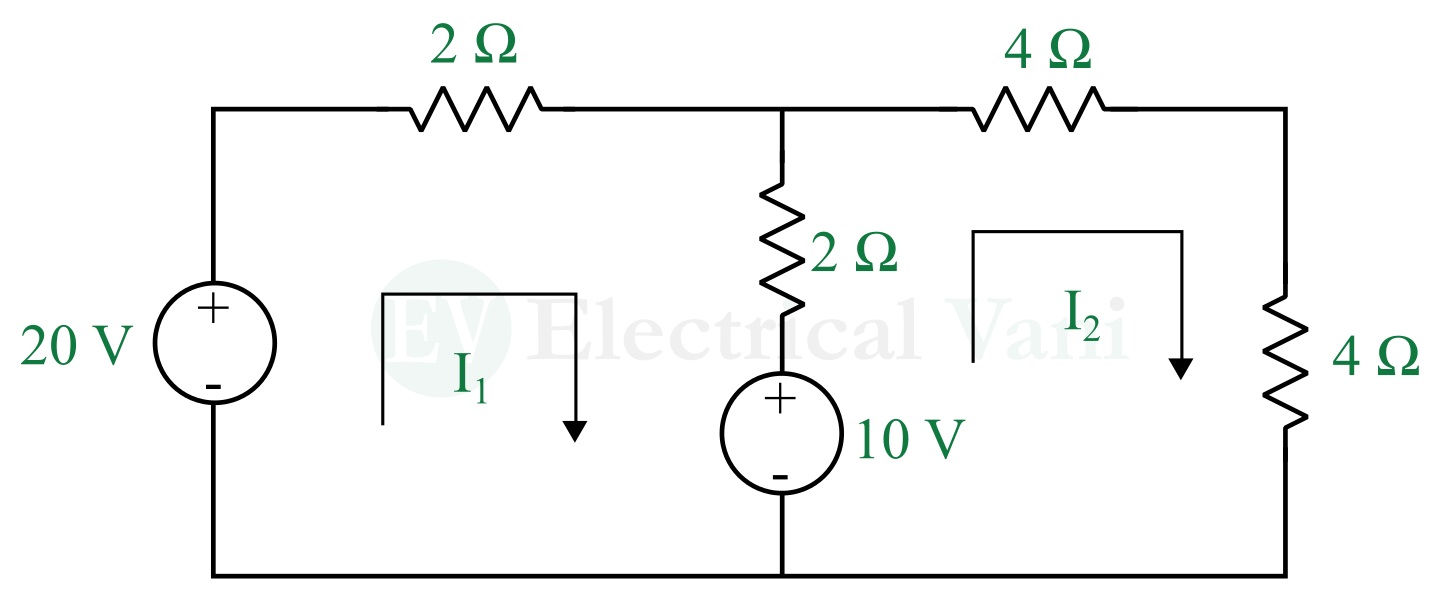
In mesh-1, applying KVL, we get,
$$20-2I_1-2(I_1-I_2 )-10=0$$
$$⇒4I_1-2I_2=10…(1)$$
In mesh-2, applying KVL, we get,
$$10-2(I_2-I_1 )-4I_2-4I_2=0$$
$$⇒-2I_1+10I_2=10…(2)$$
Solving equations (1) and (2) simultaneously, we get,
$$I_1=3.33\text{ A}$$
$$I_2=1.67\text{ A}$$
Mesh Analysis with Current Sources
In this section, we will learn how to apply mesh analysis to circuits containing current sources. Mesh analysis of a circuit containing current sources is much easier than the previous case because the presence of current sources reduces the number of simultaneous equations.
There can be the following two possible cases in mesh analysis with current sources:
Case I – When the current source exists only in one mesh as shown in the following figure.

In this case, the mesh equations will be,
In mesh 1, applying KVL, we get,
$$5-2I_1-4(I_1-I_2 )=0$$
In mesh 2, we get,
$$I_2=-2\text{ A}$$
The rest procedure for solving this circuit is similar to the previous one.
Case II – There is another case in which a current source exists between two meshes. This is the case of super mesh. Where, a super mesh is formed when two meshes share a common current as shown in the following figure.
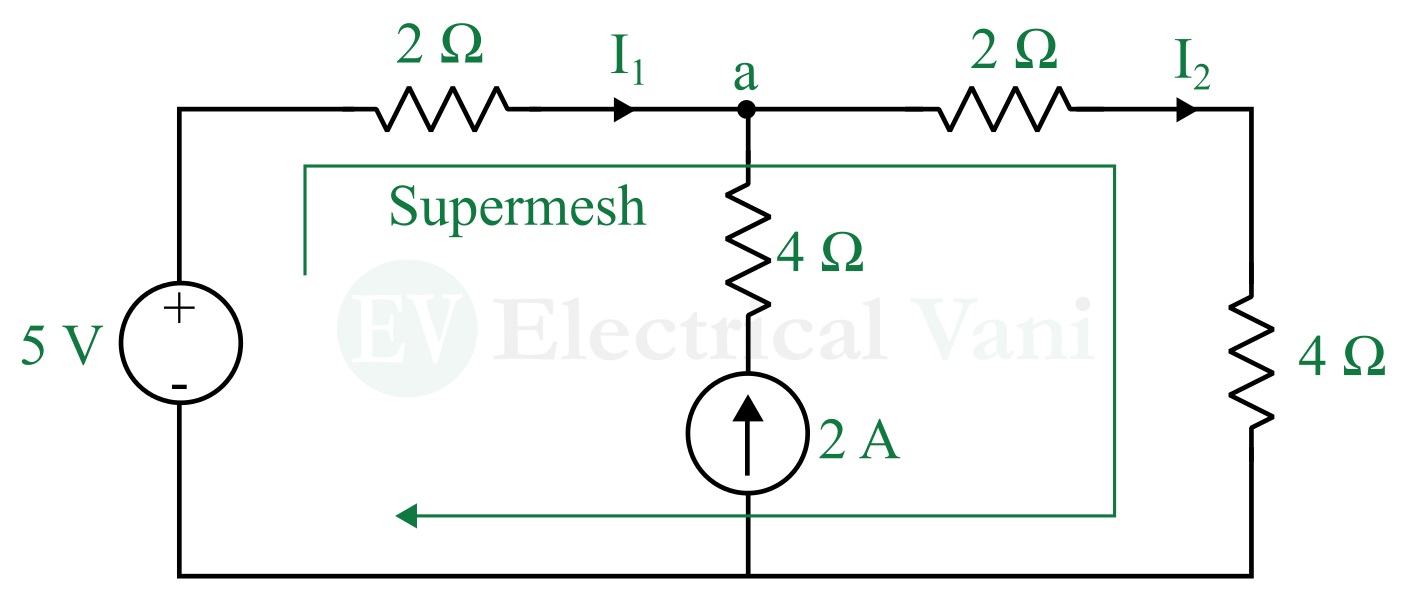
To solve super mesh, we need to apply both KCL and KVL to the circuit.
As in this circuit, applying KCL at node (a), we get,
$$I_1+2=I_2$$
By applying KVL in the super mesh, we get,
$$5-2I_1-2I_2-4I_2=0$$
Substituting the value of I2, we get,
$$5-2I_1-2(I_1+2)-4(I_1+2)=0$$
$$⇒5-2I_1-2I_1-4-4I_1-8=0$$
$$∴I_1=0.875\text{ A}$$
And current I2 is,
$$I_2=0.875+2=2.875\text{ A}$$
This is how we apply mesh analysis to circuits containing current sources.
Conclusion
This is all about mesh analysis. In this article, we have learned about mesh analysis and its different cases. More specifically, we have covered mesh analysis of circuits containing voltage sources, mesh analysis of circuits containing current sources, and mesh analysis with super mesh. After learning this concept, you should try to solve numerical problems based on it.